Patní deska - ohybová tuhost
Počáteční ohybovou tuhost patky lze stanovit při různé historii zatěžování. Nejběžnější je proporcionální zatěžování s konstantní excentricitou osové síly e= MEd/NEd= konst. Méně běžné je vyjádření tuhosti při konstantní osové síle v patce (Bowman, 1989).
Následující model tuhosti je odvozen pro výše uvedené zjednodušení působiště tlakových reakcí pod pásnicemi sloupu. Závislost deformace δt, δc jednotlivých komponentů na vnitřních silách závisí na tuhosti tažené části kt a tlačené části patky kc a vyjádří se jako
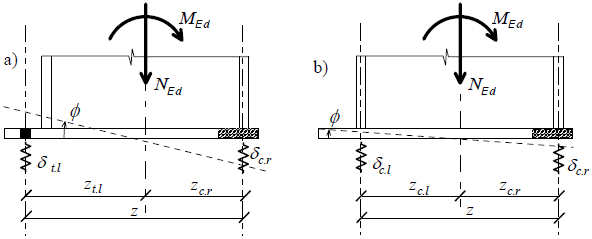 Mechanický model patky
Mechanický model patky
![]()
![]()
S využitím předcházejících vztahů můžeme určit natočení patní desky
![]()
a z něho vyjádřit počáteční ohybovou tuhost jako
![]()
Nelineární část závislosti momentu na natočení se podobně jako u jiných styčníků modeluje tvarovým součinitelem dle EN 1993-1-8 ve tvaru
![]()
Sečná ohybová tuhost se stanoví jako
![]()
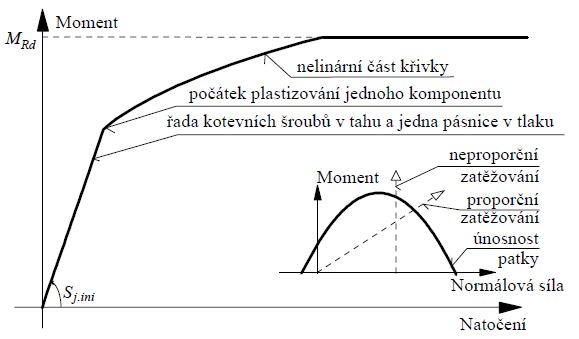 Závislost natočení na momentu pro proporční zatěžování s konstantní excentricitou
Závislost natočení na momentu pro proporční zatěžování s konstantní excentricitou
Lineární část křivky reprezentuje namáhání řady kotevních šroubů u jedné pásnice sloupu tahem s druhou pásnicí v tlaku. Nelineární část křivky začíná při plastizování jednoho z komponentů, buď patní desky a šroubů v tahu nebo betonu v tlaku.
Na následujícím obrázku je dokumentován vliv zjednodušeného modelu na stanovení únosnosti. Je vidět, že navrhované zjednodušení je konzervativní a pro podrobné posouzení není vhodné.
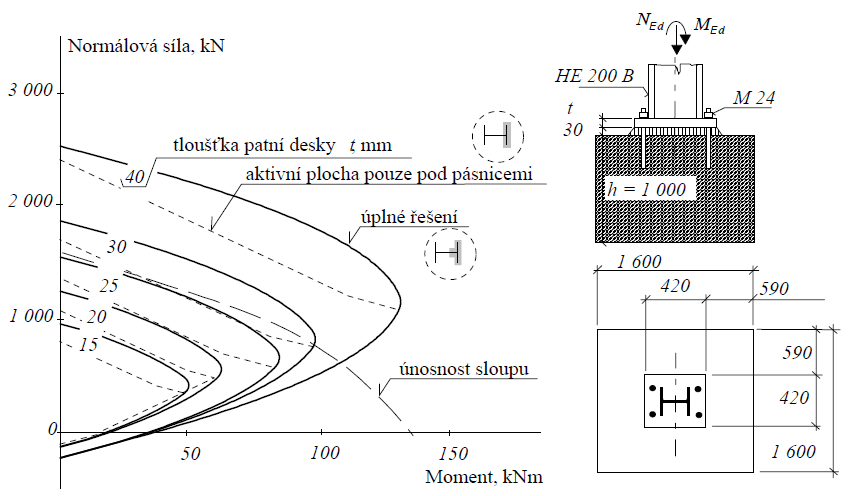 Porovnání únosnosti zjednodušeného modelu s aktivní plochou pouze pod pásnicemi sloupu (změny křivosti jsou způsobeny aktivováním šroubu), s modelem zahrnujícím aktivní plochu pod celým průřezem sloupu
Porovnání únosnosti zjednodušeného modelu s aktivní plochou pouze pod pásnicemi sloupu (změny křivosti jsou způsobeny aktivováním šroubu), s modelem zahrnujícím aktivní plochu pod celým průřezem sloupu
Literatura
Bowman L P, Gresnight A. M., Romeijn, A: Reserch into the connection of steel base plate to concrete foundation, holandsky, Stevin Laboratory Report No.: 25.6.89.05/c6, Delft 1989.