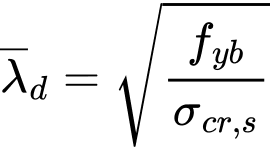Výpočet efektivního průřezu tenkostěnných za studena tvarovaných profilů
Na každém počítaném řezu zatíženém kombinací normálové síly N a ohybových momentů My a Mz se stanoví tři efektivní průřezy:
- efektivní průřez od zatížení pouze tlakovou silou N, využije se pro stanovení únosnosti v tlaku,
- efektivní průřez od zatížení pouze ohybovým momentem My, využije se pro stanovení únosnosti v ohybu.
- efektivní průřez od zatížení pouze ohybovým momentem Mz, využije se pro stanovení únosnosti v ohybu.
Výpočet efektivního průřezu tenkostěnných za studena tvarovaných profilů se provádí v následujících krocích.
Výpočet účinných šířek na tlačených pásnicích s okrajovými výztuhami
V prvním kroku se provede výpočet počátečních účinných šířek be1 a be2 na pásnici s okrajovou výztuhou znázorněné na obrázku 5.7. Výpočet se provádí podle EN 1993-1-5, kapitoly 4.4 a tabulky 4.1. Pro výpočet účinné šířky stanovíme součinitel boulení ρ dle 4.4(2), pomocí kterého zredukujeme šířku pásnice. Počáteční hodnoty účinných šířek ceff a deff vyznačených na obrázku 5.7 se mají určit podle EN 1993-1-3, 5.5.3.2(5).
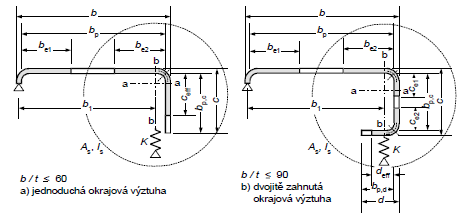 Obrázek 5.7 Okrajové výztuhy
Obrázek 5.7 Okrajové výztuhy
V druhém kroku se stanoví součinitel vzpěrnosti pro distorzní ztrátu stability (rovinné vybočení výztuhy) pro účinný průřez z kroku 1 za předpokladu působení spojitého pružného podepření následovně:
Výpočet kritického napětí na rovinné části s okrajovými výztuhami
Výpočet kritického napětí na rovinné části s krajní výztuhou se provádí dle EN 1993-1-3, 5.5.3.2(7)
Pro rovinné části s okrajovou výztuhou je pružné kritické napětí σcr,s stanoveno ze vztahu (5.15):
![]()
kde: | K | je pérová tuhost výztuhy na jednotkovou délku, viz. 5.5.3.1(2) |
As, Is | plocha a moment setrvačnosti průřezu výztuhy podle obrázku 5.7. |
Účinná průřezová plocha okrajové výztuhy As se získá ze vztahu (5.14a) nebo (5.14b):
![]() nebo
nebo
![]()
Výpočet součinitele χd pro únosnost v distorzním vybočení
Součinitel χd se stanoví dle EN 1993-1-3, 5.5.3.1 (7), rovnic (5.12a), (5.12b), (5.12c), (5.12d):
| pro |
| |
| pro |
| |
| pro |
| |
kde |
|
Výpočet účinné šířky na stojině
Pro výpočet účinné šířky stojiny postupujeme podle EN 1993-1-5, kapitoly 4.4 a tabulky 4.1 a to tak, že stanovíme součinitel boulení ρ dle 4.4(2) za pomocí kterého zredukujeme šířku stojiny.
Ve třetím kroku se iteračním postupem doladí efektivní šířky a hodnota součinitelů vzpěrnosti pro vybočení výztuh.
Je-li χd < 1, použijí se pro výpočet efektivních šířek modifikované hodnoty ρ získané dle 5.5.2(5), kde se σcom,Ed,i rovná χd fyb/γM0, takže platí:
![]()
Iterace se opakuje maximálně 3x, případně se ukončí dříve při dosažení 1% rozdílu efektivních ploch ve dvou po sobě jdoucích iteracích.
Stanovení efektivního průřezu
Efektivní průřez vznikne redukcí plného průřezu kombinací následujících dvou způsobů:
- Zavedením otvorů (děr) na tlačených pásnicích a stojinách na základě účinných šířek jednotlivých rovinných částí vypočítaných iteračním postupem viz výše,
- Zavedení ztenčení na tlačených výztuhách a přiléhajících rovinných částech. Ztenčení se vyjádří pomocí redukované tloušťky tred, dle EN 1993-1-3, 5.5.3.2(12):
![]()
kde redukovaná účinná plocha výztuhy As,red pro výpočet únosnosti při rovinném vybočení se má vzít podle 5.5.3.2(11) jako:
![]() ale
ale
![]()
kde σcom,Ed je tlakové napětí určené na základě účinného průřezu pro těžiště výztuhy.
Příklady efektivních průřezů tenkostěnných za studena tvarovaných profilů
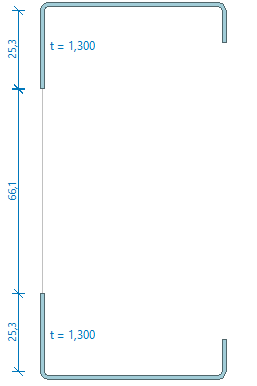
- Efektivní průřez od normálové síly
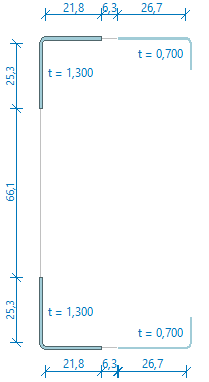
- Efektivní průřez od ohybového momentu My

- Efektivní průřez od ohybového momentu Mz