Guida Online

Výpočet podle 2. řádu

Teoretický úvod

S rozvojem moderní výpočetní techniky se teorie druhého řádu stává mocným nástrojem inženýra při navrhování štíhlých prutových konstrukcí. Názory na rámec jejího použití se však v inženýrské komunitě často různí. V této kapitole se proto pokusíme objasnit některé důležité aspekty této teorie jak z hlediska teoretického tak z hlediska jejího praktického využití.

Jak jsme se již v úvodu této kapitoly zmínili, je teorie druhého řádu aparát k analýze napjatosti štíhlých konstrukcí s výraznými osovými silami, které se nacházejí buď pod účinkem příčných sil nebo jsou vystaveny vlivu počátečních imperfekcí. Imperfekce mohou být materiálové (např. nerovnoměrné rozložení tuhostí po průřezu) nebo geometrické (zakřivená osa prutu před zatížením, excentricity v uložení pilířů ap.). Materiálové imperfekce lze obvykle převést na imperfekce geometrické. V takovém případě chápeme osu v imperfektní konstrukci jako spojnici středů tuhostí heterogenních průřezů.

Teorie druhého řádu je zjednodušením metod geometricky nelineární analýzy konstrukcí. Předpoklady, na kterých je tato teorie vybudována, jsou uvedeny níže. Zde se nejprve stručně zmíníme o rozdílu mezi geometricky nelineárním a lineárním přístupem, jako i o možnostech jejich praktické aplikace. K ilustraci postačí následující obrázek

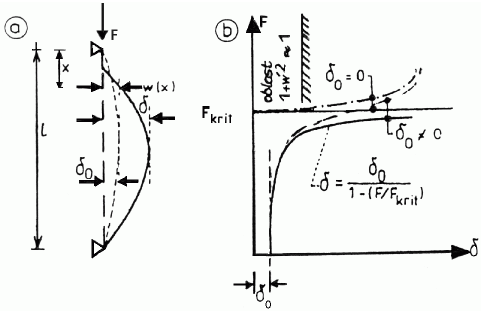Zatěžovací dráhy dokonalého (δ₀=0) a imperfektního prutu (δ₀≠0)

V první části obrázku jsou počáteční imperfekce vyjádřeny parametrem δ₀, konečý stav parametrem δ. Přpomeňe, že počáteční imperfekce δ₀ mohou být způsobeny i účinkem příčných sil. Stanovíme je obvyklým výpočtem při zanedbání osových sil na přetvoření konstrukce (teorie prvního řádu). V části b jsou načtnuty zatěžovací dráhy dokonalého (δ₀=0) a imperfektního (δ₀≠0) prutu odpovídající geometricky nelineárnímu (čerchované křivky) a lineárnímu (plné křivky) řešení. Lze je získat integrací Eulerovy diferenciální rovnice

kde v geometricky nelineární úloze platí

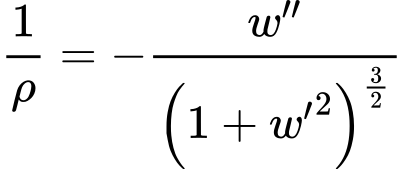
a v lineární úloze platí

Čárkou je označena derivace průhybu podle x. I za použití zjednodušení je při složitém tvaru konstrukce integrace Eulerovy diferenciální rovnice  obtížná, a proto se používají různé přibližné metody. Podobně jako v případě teorie prvního řádu je i zde použita deformační varianta MKP.

Geometricky nelineární výpočty jsou nezbytné k nalezení kritických stavů (bifurkačních či limitních) na dráze "zatížení-posun" zejména u konstrukcí zakřivených, jako jsou oblouky a prutové mřížoviny uspořádané do tvaru zakřivené plochy (např. kulové či válcové ap.). V limitním bodě zatížení dosahuje své maximální nebo minimální hodnoty ("bod zvratu"), v bifurkačním bodě dochází k rozvětvení rovnováhy (např. vedle rovnováhy na symetricky se deformující oblouk - plná čára, může existovat rovnováha na nesymetricky se deformujícím oblouku - čárkovaná čára). Tyto vztahy nelze v žádném případě zachytit lineárním výpočtem (čerchovaná čára), který výrazně nadhodnocuje stabilitní únosnost konstrukce.

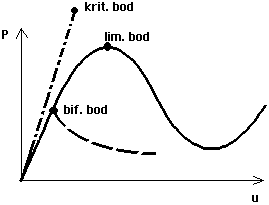Bifurkační a limitní body

Lineární výpočty lze naproti tomu aplikovat s jistotou u klasických rámových konstrukcí tvořících ortogonální systém (a na následujícím obrázku). Zatímco konstrukce na na pozici a umožňuje linearizaci výpočtu, vzpěradlo na pozici b se svým chováním blíží spíše oblouku (pozice c) a linearizace je nepřípustná. Rozhodnutí, zda konstrukci lze řešit lineárním či nelineárním výpočtem, vyžaduje nejen určité teoretické znalosti, ale i jisté praktické zkušenosti inženýra.

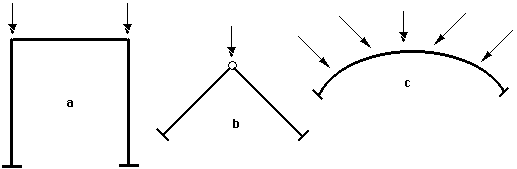Využitelnost lineární teorie

Předpoklady teorie 2.řádu

Teorie druhého řádu je zjednodušením geometricky lineárního výpočtu spočívající na těchto předpokladech

• Lze linearizovat geometrické vztahy mezi deformacemi a posuny (geometricky lineární výpočet).
• Rozložení osových sil se při deformaci konstrukce nemění.
• Rovnováha se vyjadřuje na deformovaném tvaru.

Při klasické formulaci založené na integraci základních rovnic lze vyjádřit vztah mezi koncovými silami prutu f a odpovídajícími posuny r ve tvaru

Poznamenejme, že při proporcionálním zatížení všechny vnější síly rostou úměrně tomuto parametru. Linearita úlohy spočívá v tom, že matice tuhosti K není funkcí vektoru uzlových deformací r . Úlohu lze řešit dvěma způsoby.

1. Matici tuhosti K(λ) uvedeme na tvar

Rozložíme-li konstrukci na dostatečný počet prvků, blíží se řešení s rozvojem k přesnému řešení. Tento postup je základem programů systému FIN 3D a FIN 2D. V souladu s výše uvedenou formulací probíhá výpočet následujícím způsobem. V prvním kroku se pro předpokládané zatížení určí průběh normálových sil po konstrukci užitím teorie prvního řádu. Znalost normálových sil pro dané zatížení slouží k sestavení matice počátečních napětí K_σ. Statický výpočet se pak opakuje, tentokrát však s modifikovanou maticí K(λ).

Základní rovnice předpokládá ideální tvar konstrukce, ovšem s možností zatížení příčnými silami. V případě imperfektní konstrukce zatížené osovými silami nejprve nabude rovnice základní rovnice s výše uvedenou úpravou tvaru

Výraz K₀r₀ je ekvivalentní účinku příčných sil. V případě kombinací obou se silové účinky imperfekcí K₀r₀ i příčných sil R sčítají. Pokud jsou na druhé straně oba výrazy jak K₀r₀ a R rovny nule, přejde rovnice na problém lineární stability.

2. Druhý přístup (iterační) odráží klasické přístupy analýzy imperfektních štíhlých konstrukcí:

Řeší se úloha

Matice tuhosti se opraví s ohledem na novou (aktualizovanou) geometrii, takže

Nerovnováhu f≠K₁r je třeba rozvést pomocí rovnice

neboli

Výpočet se opakuje až

Vztah teorie druhého řádu k normám

Normový výpočet vyžaduje stanovení součinitele vzpěrnosti, který se opírá o stanovení štíhlosti prutu (vzpěrné délky). Je třeba zdůraznit, že příslušné vztahy vycházejí z předpokladu, že se jedná o chování izolovaného prutu. Z tohoto důvodu jsou také velmi obtížně použitelné, zejména pokud se jedná o složitější konstrukci, v níž jsou některé pruty tlačené a jiné tažené, takže tvar vybočení těchto prutů se zásadně liší. Pro tyto účely poskytuje na druhé straně výpočet podle teorie druhého řádu vnitřní síly na přetvořené konstrukci, takže výpočet napětí nevyžaduje stanovení součinitelů vzpěrnosti. Lze říci, že stabilitní výpočet se tak převádí na výpočet pevnostní.

Závěrem tohoto odstavce upozorníme na jeden důležitý poznatek. Známe-li hodnotu součinitele kritického zatížení λ_krit, můžeme snadno odhadnout při proporcionálním zatížení a za předpokladu, že rozhodující pruty jsou převážně tlačené, přetvoření podle teorie druhého řádu vzhledem k počátečním imperfekcím δ₀ popřípadě k deformacím vypočteným podle teorie prvního řádu.

Obdobný vztah, byť s menší přesností, platí i pro vnitřní síly, např. ohybové momenty.

V tomto vzorci se odráží smysl výpočtu kritického zatížení.

K posouzení platnosti vztahů uvedených výše jsme zvolili příklad jednoduchého rovinného rámu zatíženého osamělými silami v rámových rozích. Předpokládané geometrické imperfekce byly modelovány příčnými silami velikosti 1/100 svislého zatížení. Vodorovný posun příčle δ₀ vypočtený podle teorie prvního řádu byl v tomto případě roven 0,659mm. Výpočet podle teorie druhého řádu vedl k hodnotě příčného posunu δ rovné 0,675mm. Obdobné výsledky jsme obdrželi pro hodnoty ohybových momentů ve vetknutí. Moment M₀ byl roven 1.66kNm, zatímco moment M vypočtený podle teorie druhého řádu vzrostl na 1,69kNm. Při použití výše uvedených rovnic jsme obdrželi hodnotu příčného posunu δ rovnu 0,676mm, což se prakticky shoduje s výpočtem pomocí programu FIN 3D. Hodnota ohybového momentu je rovna 1,70kNm . V porovnání s výpočtem je tento rozdíl méně než 0,6%.

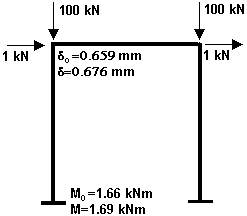Zadání příkladu

Závěrem bychom chtěli poznamenat, že i přes efektivní výpočetní techniku a programy by inženýr neměl zapomínat na jednoduché metody výpočtu, které mu poskytnou rychlý odhad chování imperfektní konstrukce, zejména při předběžném návrhu.