0

FIN EC software

Guida Online

Tree
Impostazioni
Programmi:
Lingua:

Buckling

The second order effects are taken into account for the members loaded by compressive force in accordance with the chapter 5.8 of EN 1992-1-1. Following methods are avalable:

  • Method based on the nominal stiffness
  • Method based on the nominal curvature
  • Simplified method based on 12.6.5.2 of the standard (only plain concrete)

Slenderness criterion

The detailed analysis is performed if the slenderness is greater than limiting value λlim. The limiting slenderness is given by the expression 5.13N:

Where is:

λlim

  • The limiting slenderness

A, B, C

  • The coefficients

n

  • The relative normal force

The coefficient A is given by the expression:

Where is:

φef

  • The effective creep ratio

The coefficient B is given by the expression:

Where is:

ω

  • The mechanical reinforcement ratio

The mechanical reinforcement ratio ω is given by the expression:

Where is:

As

  • The total area of longitudinal reinforcement

fyd

  • The design yield strength of reinforcement

Ac

  • The cross-sectional area

fcd

  • The design compressive strength of concrete

The coefficient C is given by the expression:

Where is:

rm

  • The moment ratio

The moment ratio rm is given by the expression:

Where is:

M01, M02

  • The first order end moments

The relative normal force n is given by the expression:

Where is:

NEd

  • The design value of the normal force

Ac

  • The cross-sectional area

fcd

  • The design compressive strength of concrete

Method based on the nominal stiffness

This method is based on the chapter 5.8.7. The nominal stiffness is given by expression (5.21):

Where is:

Kc

  • The factor for effects of cracking, creep etc.

Ecd

  • The design value of the modulus of elasticity of concrete

Ic

  • The moment of inertia of concrete cross section

Ks

  • The factor for contribution of reinforcement

Es

  • The design value of the modulus of elasticity of reinforcement

Is

  • The second moment of area of reinforcement, about the centre of area of the concrete

The factor Kc is given by expression (5.22):

Where is:

k1

  • The factor which depends on concrete strength class

k2

  • The factor which depends on axial force and slenderness

φef

  • The effective creep ratio

The factor k1 is given by expression (5.23):

Where is:

fck

  • The characteristic compressive cylinder strength of concrete at 28 days

The factor k2 is given by expression (5.24):

Where is:

n

  • The relative axial force

λ

  • The slenderness ratio

The buckling load based on the nominal stiffness is calculated using expression:

Where is:

NB

  • The buckling load based on nominal stiffness

EI

  • The nominal stiffness

l0

  • The effective length for buckling analysis

The total design moment, including second order moment, is calculated using formula (5.28):

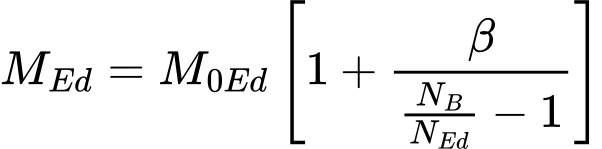
Where is:

M0Ed

  • The first order moment

β

  • The factor that depends on distribution of first and second order moments

NB

  • The buckling load based on nominal stiffness

NEd

  • The design value of axial load

The factor β is given by expression (5.29):

Where is:

c0

  • The coefficient which depends on the distribution of first order moment

The value of the factor c0 is the input in the software. Following values are recommended according to the chapter 5.8.7.3(3):

Factor c0

The distribution of first order moment

8.0

constant

9.6

parabolic

12

symmetric triangular

Method based on the nominal curvature

This method uses procedures given in the chapter 5.8.8. The nominal curvature is given by the expression (5.34):

Where is:

1/r

  • The curvature

Kr

  • The correction factor depending on axial load

Kφ

  • The factor for taking account of creep

The curvature 1/r0 is given by following formula:

Where is:

ε0

  • The strain of reinforcement at yield strength

d

  • The effective depth of a cross-section

The strain of reinforcement at yield strength ε0 is calculated using this formula:

Where is:

fyd

  • The design yield strength of reinforcement

Es

  • The design value of modulus of elasticity of reinforcing steel

The effective depth of a cross-section is given by the expression (5.35):

Where is:

h

  • The height of a cross-section

is

  • The radius of gyration of the total reinforcement area

The factor Kr is given by the expression (5.36):

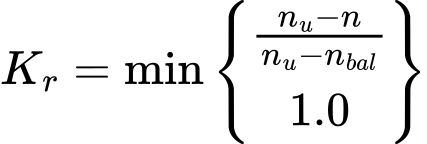
Where is:

n

  • The relative axial force

nbal

  • The value of the relative axial force at maximum moment resistance. The value 0.4 is usedin aaccordance with 5.8.8.3(3).

The relative axial force nu is calculated using the formula:

Where is:

ω

  • The mechanical reinforcement ratio

The factor Kφ is given by the expression (5.37):

Where is:

β

  • The factor depending on the strength class of the concrete and the slenderness ratio

φef

  • The effective creep ratio

The factor β is given by the expression:

Where is:

fck

  • The characteristic compressive cylinder strength of concrete at 28 days

λ

  • The slenderness ratio

The nominal second order moment M2 is given by the expression (5.33):

Where is:

NEd

  • The design value of axial force

e2

  • The member deflection

he deflection e2 is calculated using formula

Where is:

1/r

  • The curvature

l0

  • The effective length for buckling analysis

c

  • The factor depending on the curvature distribution

The value of the factor c is the input in the software. Following values are recommended according to the chapter 5.8.8.2(4):

Factor c

Curvature distribution

8.0

constant

10

sinusoidal

The design moment is given by the expression (5.31):

Where is:

MEd

  • The design moment including the second order effect

M0Ed

  • The design value of the first order moment

M2

  • The nominal second order moment

Simplified design method according to 12.6.5.2

This method may be used for plain concrete and lightly reinforced members according to the chapter 12.6.5.2 of EN 1992-1-1. The design axial resistance is given by the expression (12.10):

Where is:

b

  • The overall width of the cross-section

hw

  • The overall depth of the cross-section

fcd

  • The design compressive strength of concrete

Φ

  • The factor taking into account eccentricity

The factor Φ is given by the expression (12.11):

The eccentricity etot is calculated using following formula:

Where is:

e0

  • The first order eccentricity including, where relevant, the effects of floors (e.g. possible clamping moments transmitted to the wall from a slab) and horizontal actions

ei

  • The additional eccentricity covering the effects of geometrical imperfections

l0

  • The effective length for buckling analysis

Prova il Software FIN EC. Gratuitamente, senza limitazioni di analisi.

Ulteriori strumenti per l'apprendimento GRATIS

Versione Demo

Prova il nostro software senza alcuna restrizione sulle analisi.

Video Tutorial

Guarda l'uso pratico del nostro programma.

Manuali di Ingegneria

Scarica manuali con spiegazioni teoriche e pratiche dell'uso del programma.