Calculation of the effective cross-section of cold formed cross-sections
At each calculated cross-section loaded by a combination of normal force N and bending moments My and Mz, three effective cross-sections are determined:
- the effective cross-section due to the normal force N only, is used to determine the bearing capacity in compression.
- the effective cross-section due to the bending moment My, is used to determine the bearing capacity in bending.
- the effective cross-section due to the bending moment Mz, is used to determine the bearing capacity in bending.
The calculation of the effective cross-section of cold formed cross-sections is carried out in the following steps.
Calculation of effective widths of compression flanges with edge stiffeners
The calculation of initial values of effective widths be1 and be2 shown in Fig 5.7 on flange with edge stiffener should be obtain in first step of calculation.
Calculation is carried out acc. to EN 1993-1-5, chapter 4.4 and table 4.1. The buckling reduction factor ρ which is used to reduce width of the flange is determined acc. to 4.4(2). The initial values of effective widths ceff and deff shown in Fig 5.7 should be obtain due to EN 1993-1-3, 5.5.3.2(5).
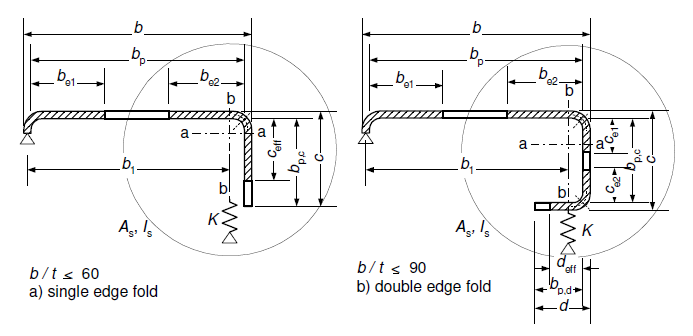Figure 5.7 Edge stiffeners
Use the initial effective cross-section from first step to determine the reduction factor for distortional buckling (flexural buckling of a stiffener), allowing for the effects of the continuous spring restraint in second step as follow:
Calculation of the critical stress on plane element with edge stiffeners
The calculation of critical stress on plane element with edge stiffener is carried out acc. to EN 1993-1-3, 5.5.3.2(7).
The elastic critical buckling stress σcr,s for plane elements with edge stiffener should be obtained from:
where | K | is the spring stiffness per unit length, see 5.5.3.1(2). |
As, Is | effective area and effective second moment of area of the stiffener due to Fig 5.7. |
The effective cross-sectional area of the edge stiffener As should be obtained from (5.14a) or (5.14b):
or
Calculation of reduction factor χd for the distortional buckling resistance
The reduction factor χd for the distortional buckling resistance should be obtained acc. to EN 1993-1-3, 5.5.3.1 (7), formulas (5.12a), (5.12b), (5.12c), (5.12d):
| for |
| |
| for |
| |
| for |
| |
where: |
|
Calculation of effective width of web
Calculation is carried out acc. to EN 1993-1-5, chapter 4.4 and table 4.1. The buckling reduction factor ρ which is used to reduce width of the web is determined acc. to 4.4(2).
Optionally iterate to refine the value of effective widths and the value of the reduction factor for buckling of the stiffener in third step of calculation.
If χd < 1, modified values of ρ obtained using 5.5.2(5) should be used for calculation of effective widths, with σcom,Ed,i equal to χd fyb/γM0, so that:
The iteration is repeated 3 times maximally or it is terminated earlier when the 1% difference of effective surfaces is reached in two consecutive iterations.
Determination of the effective cross-section
The effective cross-section is created by reducing the gross cross-section by combining the following two ways:
- By introducing openings (holes) on the compression flanges and webs based on the effective widths of the individual flat parts calculated iteratively see above,
- By introduction of the thickness reductions on compression stiffeners and on adjacent flat parts. The thickness reduction is expressed using reduced thickness tred, acc. to EN 1993-1-3, 5.5.3.2(12):
where reduced effective area of the stiffener As,red allowing for flexural buckling should be taken acc. to 5.5.3.2(11) as:
but
where σcom,Ed is compressive stress at the centerline of the stiffener calculated on the basis of the effective cross-section.
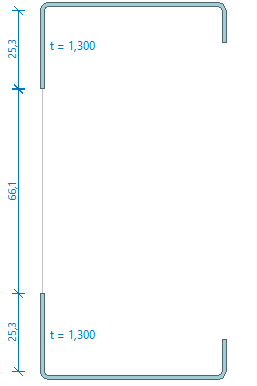
Examples of the effective cross-sections of cold formed cross-sections
- Effective cross-section due to axial force
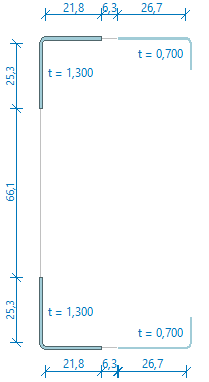
- Effective cross-section due to bending moment My
- Effective cross-section due to bending moment Mz
