Guida Online

Hypoplastischer Ton

Hypoplastischer Ton ist für modellierung der Aufgaben in der weichen, feinkörnigen Böden bestimmt. Es ist ein phänomenologisches Standardmodell und mit seinem Charakter gehört zu der kritischen Zustandsmodellen (modifiziertes Cam-Ton-Modell, Verallgemeinertes Cam-Ton-Modell). Das Modell berücksichtigt das nichtlineare Bodenverhalten sowohl bei der Belastung als auch bei der Entlastung. Im Gegensatz zu Standardmodellen, die auf der Plastizitätstheorie basieren, können jedoch nur die Gesamtdeformationen ausgedrückt werden, sodass unterschiedet nicht die elastischen und plastischen Deformationen. Der Charakter von Art und Ort des möglichen Versagens kann bei Standardmodellen, die durch den Bereich der äquivalenten deviatorischen plastischen Verformung repräsentiert wird, kann im Fall des hypoplastischen Lehms durch die Verteilung des mobilisierten inneren Reibungswinkels erfolgen.

Bei der Beschreibung der Bodenreaktion auf äußere Einflüsse berücksichtigt das Modell unterschiedliche Steifigkeiten bei der Belastung und Entlastung, Erweichen oder Verstärken in Abhängigkeit von Bodenverdichtung und Volumenänderung bei Scherverformung (Dilatanz, Kontraktion). Die tatsächliche Steifigkeit hängt nicht nur von der Richtung der Auflast ab, sondern auch vom Zustand des Bodens, der durch seine Porosität gegeben ist. Im Gegensatz zum Cam-Clay-Modell werden Zugspannungen im Boden gründlich ausgeschlossen (siehe Abbildung 1a).

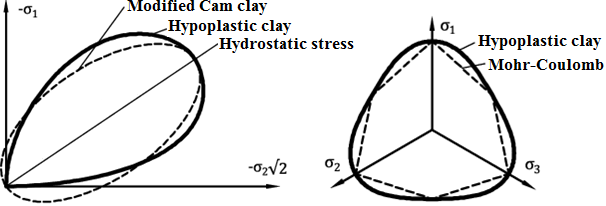Abb. 1: Zustandsgrenze des hypoplastischen Modells - (a) Vergleich mit dem Plastizitätsbereich des Cam-Clay-Modells in der Meridialebene, (b) Vergleich mit dem Plastizitätsbereich des Mohr-Coulomb-Modells in der Deviatorialebene

Im Falle des hypoplastischen Modells wird der Plastizitätsbereich durch die sogenannte Grenzzustandsfläche (Boundary state surface) ersetzt. Seine Projektion in der deviatorischen Ebene ähnelt dem modifizierten Mohr-Coulomb-Modell (siehe Abbildung 1b) Aus Sicht der Regel plastischen Kriechgesetzes handelt es sich um ein nicht assoziiertes Gesetz, das nicht symmetrischen Steifheitsmatrix der tatsächlichen Steifheit ergibt (vergleiche z. B. mit dem Mohr-Coulomb-Modell bei unterschiedlichen Werten des inneren Reibungswinkels φ und des Dilatationswinkels di). Eine detaillierte Formulierung des hypoplastischen Modells findet sich in [1].

Modellparameter

Das Grundmodell benötigt fünf Materialparameter:

• Winkel der inneren Reibung bei konstantem Volumen (kritischer Winkel der inneren Reibung) φ_cv
• Neigungslinie der Quellung κ*
• Steigung der normalen Konsolidierungslinie (NCL - normal consolidation line) λ*
• Beginn der normalen Konsolidierungslinie N
• Verhältnis von Volumen- und Schubmodul r

Die Parameter κ *, λ * und N bestimmen das bilineare Diagramm der isotropen Konsolidierung auf einer logarithmischen Skala, Abbildung 2a. Wenn bilineare Diagrammparameter für das modifizierte Cam-Clay-Modell verfügbar sind (in einem halblogarithmischen Maßstab, Abbildung 2b), können diese Werte eingegeben und die entsprechenden hypoplastischen Clay-Parameter neu berechnet werden. Die bilinearen Diagrammparameter für das modifizierte Cam-Clay-Modell:

• Steigungslinie der Quellung κ (in einem halblogarithmischen Maßstab)
• Steigung der normalen Konsolidierungslinie λ (in einem halblogarithmischen Maßstab)
• Die Porenzahl e_max für normalen Konsolidierung mit allseitigen Druck 1kPa

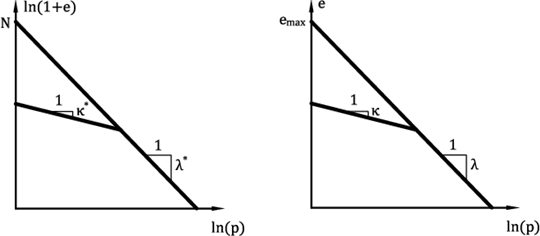Abb.2: Bilineardiagramm der isotropen Konsolidierung - (a) Hypoplastischer Ton, (b) Cam-clay-Model

Kritischer Winkel der inneren Reibung φ_cv

• Identisch für die ursprüngliche (intakte) und rekonstituierte untersuchte konsolidierte Probe
• Kann aus einem dreiachsigen Scherversuch unter Anwendung verschiedener Kammerdrücke auf eine rekonstituierte Probe bestimmt werden
• Der Versuch kann undräniert (schneller) oder dräniert werden
• Der Wert liegt normalerweise im Bereich von 18° - 35°

Neigungslinie der normalen Konsolidation λ*

• Sie wird grafisch aus der Verlauf der Belastungsphase des Ödometerversuchs oder aus isotropen Konsolidierungsversuch ermittelt, siehe Abbildung 3
• Für feste Tone ist geeignet den Versuch auf die rekonstituierte Probe durchgeführt werden
• Der Wert liegt normalerweise im Bereich von 0,04 - 0,15

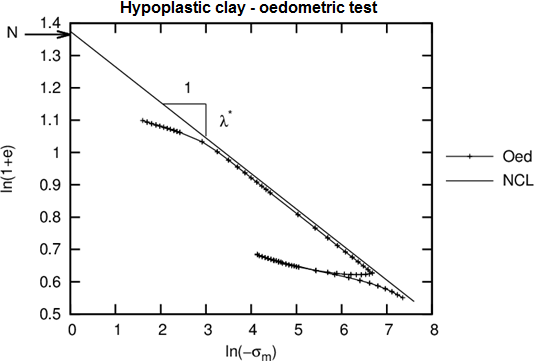Verlauf der Simulation von Ödometerversuch mit hypoplastischem Modell

Neigung der Schwellinie κ*

• Es wird durch die parametrische Studie bestimmt - Vergleich des Verlaufs von Messung und Simulation - Entlastungsphase des Ödometerversuchs oder der isotropen Konsolidierung, siehe Abbildung 3
• Der Wert κ liegt normalerweise im Bereich von 0,01 - 0,02
• Das Verhältnis λ/κ sollte größer sein als 4,0

Beginn der isotropen Konsolidierungslinie N

• Es wird grafisch aus der Verlauf der Belastungsphase des Ödometerversuchs oder der isotropen Konsolidierung bestimmt
• Der Test sollte an einer ungestörten Probe durchgeführt werden. Wenn die Lambda-Schnittlinie vertikal ist, kann die aus der rekonstituierten Probe erhaltene Lambda-Steigung bestimmt werden (siehe Abbildung 3)
• Der Wert liegt normalerweise im Bereich von 0,8 - 1,6

Verhältnis von Volumen- und Schubmodul r

• Die physikalische Bedeutung des Parameters ergibt sich aus der Beziehung r = K_i/G_i
• K_i ist das tangentialen Volumenmodul bei isotroper Komprimierung entlang der normalen Konsolidierungslinie
• G_i ist der tangentiale Schubmodul im undränierten Scherversuch bei gleicher Spannung
• Parameter r kann durch parametrische Studie des dreiachsigen Scherversuchs bestimmt werden
• Der Wert liegt normalerweise im Bereich von 0,05 - 0,7

Einstelung der anfänglichen Bodenzustand

Der Bodenzustand beim hypoplastischer Ton versteht man ihre aktuelle Verdichtung, die durch der Porenzahl ausgedrückt wird. Die Implementierung des Modells ermöglicht es Ihnen, den anfänglichen oder aktuellen Wert der Porositätszahl einzugeben oder aus der OCR-Überkonsolidierungszahl zu berechnen. Im ersten Fall ist der Wert e₀ einzugeben, der der an der aus der gegebenen Tiefe entnommenen unbelasteten Probe gemessenen Porositätszahl entspricht. Im zweiten Fall kann der e_curr Wert eingegeben werden, der der Porosität des belasteten Bodens entspricht, siehe Abbildung 4a. Die letzte Möglichkeit besteht darin, einen OCR-Wert einzugeben, der das Verhältnis zwischen der mittleren Spannung an der NCL und der tatsächlichen mittleren Spannung darstellt (siehe Abbildung 4b).

Wenn die Aufgabe in der ersten Phase durch das K_o Prozedur initialisiert wird, wird der Bodenzustand zu Beginn der nächsten Phase basierend auf der aktuellen Spannung eingestellt. Bei der Standardberechnung der ersten Phase (das hypoplastische Modell wird bereits in der ersten Berechnungsstufe eingeführt), wann der Boden mit seinem Eigengewicht belastet wird, wird bei der Einstellung des Bodenzustands der Anfangswert des mittleren Spannung pin = 1 kPa betrachtet und gilt e_curr = e₀. Wenn ein anderes Material durch einen hypoplastischen Ton ersetzt wird (z. B. das in der 1. Bauphase berücksichtigte elastische Material), wird der Spannungswert aus der vorherigen Phase berücksichtigt.

Errinern Sie, daß bei Verwendung von elastischem Material in der ersten Berechnungsstufe der anfängliche Spannungszustand den Ergebnissen des K_o Prozedur für K_o entspricht (ν ist das Poissonzahl).

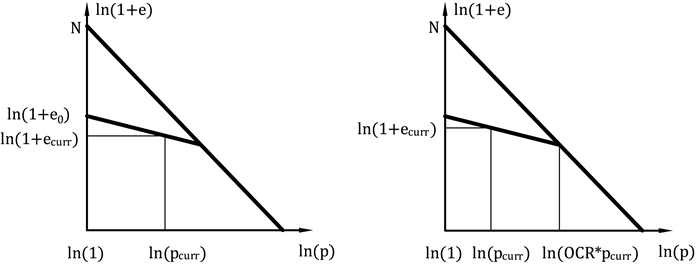Abb. 4: Initialisierung der Porenzahl - (a) unter Verwendung der anfänglichen Porenzahl, (b) unter Verwendung der OCR

Aus Abbildung 4b ist ersichtlich, daß dem normal konsolidierten Boden OCR = 1,0 entspricht, nur bei isotroper Konsolidierung, d. h. für K_o = 1,0. Liegt im konsolidierten Boden eine deviatorische Spannung ungleich Null vor, entspricht dem normal konsolidierten Boden den Wert von OCR, der höher als 1,0 wird. Der genaue OCR_NC-Wert hängt sowohl von den Bodenparametern als auch von der Richtung des Spannungslinie ab (Ko-Wert). Abb. 5 gibt einen Überblick der Abhängigkeit der minimalen OCR für verschiedene Werte von Seitendruckbeiwerten Ko und verschiedene Arten von Tonen. Spezifische Werte sind in Tabelle 1 angegeben. In Tabelle 2 sind dann die Werte der Grundparameter des hyponastischen Modells für die betrachtete Bodengruppe angegeben.

Die Wahl von OCR = 1,0 für normal konsolidierte Böden mit bis zu (K_o = 1,0) führt zu einem nicht akzeptablen Spannungszustand, der zum Verlust der Berechnungskonvergenz führen kann.

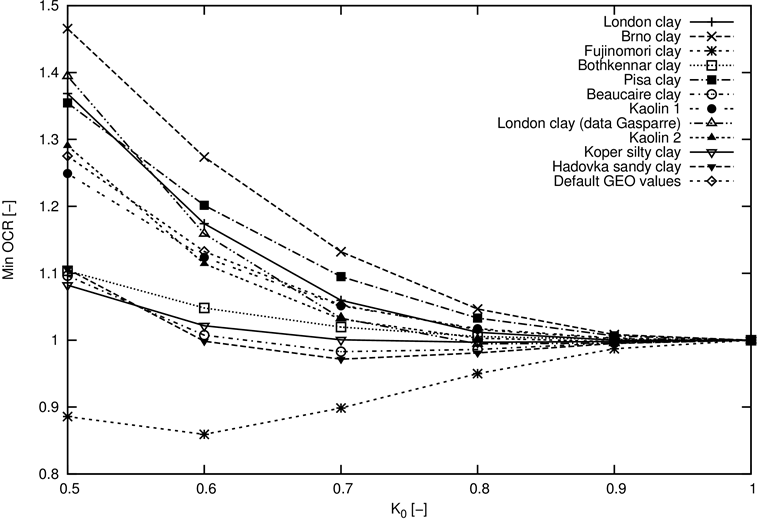Abb. 5: Abhängigkeit der minimalen OCR vom Seitendruckbeiwert im Ruhezustand K_o

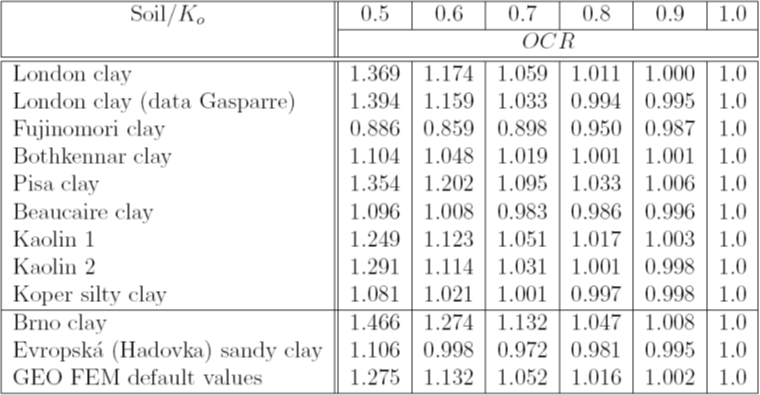Table 1: Koeffizient der Überkonsolidierung OCR ausgewählter Böden als Funktion von Ko-Wert

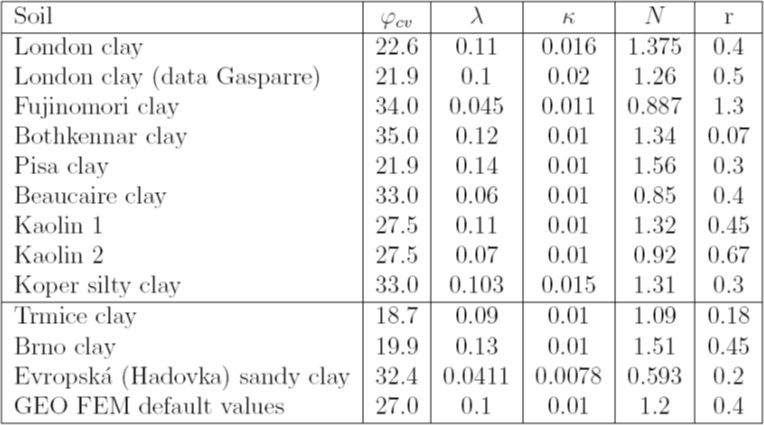Table 2: Materialparameter der ausgewählten Böden

Intergranulare Verformung

Die grundlegende Version des Modells ist für Berechnungen mit nur einer vorherrschenden Richtung der Spannungslinie geeignet. In Fällen, in denen eine zyklische Belastung auftritt, ist es ratsam, ein Modell zu verwenden, das durch intergranulare Verformung erweitert wird. Dies verringert die unerwünschte Zunahme der bleibenden Verformung, die aus kleinen wiederholten Belastungsänderung (ratcheting) resultiert. Die Einführung der intergranularen Verformung ermöglicht es, die hohe Steifigkeit modellieren, die Tone im Bereich der sehr kleinen Verformungen aufweisen. Diese Option ist in keinem der anderen Modelle enthalten, die im GEO FEM-Programm implementiert sind. Das Konzept der intergranularen Verformung setzt voraus, daß die gesamte Bodenverformung aus einer geringen elastischen Verformung der Schicht zwischen den Körnern (intergranulare Verformung) und weiter die Verformungen, die durch der gegenseitigen Verschiebung der Körner verursacht sind. Bei der Änderung der Belastungsrichtung ändert sich zunächst die intergranulare Verformung. Wenn die intergranulare Verformung ihren Grenzwert erreicht, tritt die Verformung aufgrund einer Kornverschiebung auf.

Die Verwendung des Konzepts der intergranularen Verformung erfordert fünf zusätzliche Materialparameter:

• Spannweite der elastischen intergranularen Verformung R
• Parameter m_R und m_T kontrolieren die Steifigkeit bei kleinen Verformungen
• Die Parameter β_r und χ kontrolieren den Grad der Degradation der Steifheit mit zunehmender Verformung

Diese Parameter werden mit bereits bekannten Parametern des hypoplastischen Grundmodells kalibriert.

Spannweite der elastischen intergranularen Verformung R

• Gibt das maximale Ausmaß der intergranularen Deformation an
• Kann durch die parametrische Untersuchung der Abbaukurve der Steifigkeit G = G(ε_s) bestimmt werden, siehe Abb. 5
• Alternativ kann es als materialunabhängige Konstante betrachtet werden R = 10^-4
• Der Wert liegt normalerweise im Bereich von 2_*10^-5 - 1_*10^-4

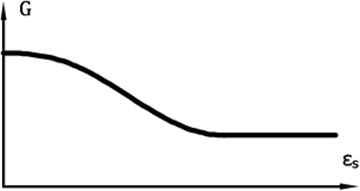Abb.6: Abbaukurve des Schermoduls

Parameter m_R

• Sie bestimmt die Größe des Schermoduls bei der Änderung der Linie der Lastspannung in der Meridionalebene (σ_m - J) o 180°
• Lineare Beziehung zwischen m_R und anfänglichen Schubmodul G₀ = p_*(m_r/(r_* λ*)
• Das anfängliche Schermodul kann durch eine geeignete Methode der Scherwellenausbreitung bestimmt werden, siehe Abb. 6.
• Der Wert liegt normalerweise im Bereich von 4,0 - 20,0

Parameter m_T

• Sie bestimmt die Größe des Schermoduls bei der Änderung der Linie der Lastspannung in der Meridionalebene (σ_m - J) o 90°
• Es gilt m_R/m_T = G₀/G₉₀
• Das anfängliche Verhältnis der Module kann aus dem Verhältnis der Module bei größeren Verformungen ermittelt werden. Der Wert der m_R/m_T-Verhältnis bewegt sich üblicherweise im Bereich von 1,0 bis 2,0
• Der Wert m_T liegt normalerweise im Bereich von 2,0 - 20,0

Parametern β_r und χ

• Sie bestimmen die Abbaugeschwindigkeit der Steifigkeit bei zunehmender Verformung
• Kann durch die parametrische Untersuchung der Abbaukurve der Steifigkeit G = G(ε_s) bestimmt werden
• Der Parameter β_r liegt normalerweise im Bereich von 0,05 - 0,5
• Der Parameter χ liegt normalerweise im Bereich von 0,5 - 6

Zu der parametrischen Studien können folgende Beispiele verwendet werden.

Literatur:

[1] D. Mašín, A hypoplastic constitutive model for clays, International Journal for Numerical and Analytical Methods in Geomechanics., 29:311-336, 2005.