Guida Online

Arcilla hipoplástica

La arcilla hipoplástica es aplicable para modelar suelos blandos de grano fino. Al igual que en el resto de modelos que pertenece a la familia de los modelos estándar de fenomenológicas. En cuanto a la descripción de la respuesta del suelo cae dentro del grupo de modelos de estado crítico (Cam clay, Cam clay generalizado).

Este modelo, sin embargo, representa la respuesta no lineal de los suelos, cargados y no cargados. En comparación con otros modelos basados ​​en la teoría de la plasticidad, que permite sólo el cálculo de total de tensión.

Por lo tanto, no hay diferencia entre las tensiones elástica y plástica. La indicación del tipo y localización de un fallo potencial, en otros modelos proporcionados por la trama de tensión equivalente plástica desviadora, puede ser en el caso de la arcilla hipoplásica representada por la distribución del ángulo de fricción interna movilizado.

Cuando se describe la respuesta del suelo, el modelo permite reflejar una rigidez diferente en carga y no carga, ablandamiento o endurecimiento en dependencia de la compactación del suelo y el cambio de volumen en corte (dilatación, compresión). La rigidez actual depende no sólo de la dirección de la carga, sino también sobre el estado actual de suelo determinado por su porosidad. A diferencia de modelos de Cam clay, estrictamente se excluyen tensiones de tracción en el suelo, véase la Figura 1a.

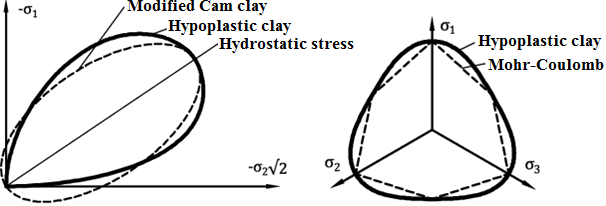Figura 1: Estado límite de modelo hipoplástico - (a) comparación con la superficie de fluencia de modelo Cam clay en el plano meridiano, (b) comparación con la superficie de fluencia de modelo de Mohr-Coulomb en el plano desviador

En el caso del modelo hipoplástico la superficie de fluencia estándar se sustituye por la superficie de estado límite. Su proyección en el plano desviador es similar a la del modelo, véase la figura 1b. La regla de flujo no se asocia a la resultante en una matriz de rigidez no simétrica (comparar por ejemplo con el modelo de Mohr-Coulomb al tener diferentes valores para el ángulo de fricción interna φ y el ángulo dilatación ψ). Los detalles relacionados a la formulación del modelo se pueden encontrar en [1].

Parámetros del modelo

La variante básica del modelo requiere entrada de cinco parámetros de material

• Ángulo de fricción interna para volumen constante (ángulo crítico de fricción interna) φ_cv
• Pendiente de la línea de hinchazón κ*
• Pendiente de la línea de consolidación normal (NCL - línea de consolidación normal) λ*
• Origen de la línea de consolidación normal N
• Relación de módulos de unidad y corte r

Los parámetros κ*, λ* y N determinan un diagrama bilineal de consolidación isótropa en la figura 2a escala logarítmica log-log . Los parámetros del modelo bilineal Cam clay (en escala semi-logarítmica, figura 2b) están disponibles, es posible introducir estos valores y los parámetros del modelo hipoplástico se re calculan. Los parámetros del modelo bilineal Cam clay son:

• Pendiente de la línea de hinchazón κ (en escala semi-logarítmica)
• Pendiente de la línea de consolidación normal λ (en escala semi-logarítmica)
• relación de vació e_max para consolidación normal isotrópica por presión de 1kPa

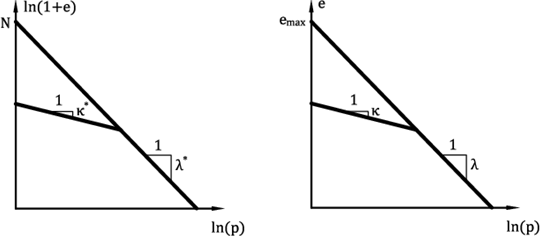Figura 2: Diagrama bilineal de consolidación isotrópica - (a) hipoplástico arcilla, (b) modelo Cam clay

Ángulo crítico de fricción interna φ_cv

• Idéntico para la muestra original (sin molestias) y la muestra consolidada reconstruida posteriormente
• Puede determinarse a partir de prueba estándar triaxial aplicando presiones diferentes de celdas en una muestra reconstituida
• Se puede realizar tanto pruebas drenadas y no drenadas (más rápido)
• Los valores más comunes están en el rango de 18 ° - 35 °

Pendiente de la línea de consolidación normal de λ*

• Se determina gráficamente a partir de la carga de la carga, de la prueba de consolidación edométrico o isotrópica, véase la figura 3
• Para arcillas rígidas, es preferible ejecutar la prueba en una muestra reconstituida
• Los valores más comunes están en el rango de 0,04 a 0,15

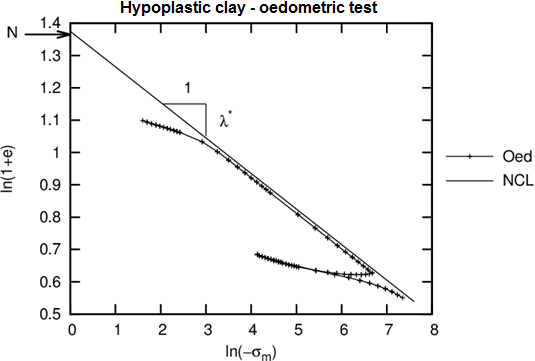Figura. 3: Simulación de pruebas con el modelo edométrico hipoplástico

Pendiente de la línea de hinchazón κ*

• Se puede determinar de manera similar al parámetro λ* gráficamente o mediante la realización de un estudio paramétrico - comparación de las mediciones y la simulación a lo largo de la descarga de prueba de consolidación edométrico o isotrópica, véase la figura 3
• Los valores más comunes de κ están en el rango de 0,01 a 0,02
• Porcentaje de λ/κ debe ser grande que 4,0

Origen de la línea de consolidación normal, N

• Se determina gráficamente a partir de la rama cargada con la prueba edométrica o de consolidación isotrópica
• La prueba se debe realizar en una muestra sin perturbaciones - Al buscar la línea de intersección lambda con el eje vertical es posible determinar la pendiente de lambda obtenida a partir de una muestra reconstituida, ver la Figura 3
• La mayoría de los valores comunes están en el rango 0.8 – 1.6

Relación de módulo de compresión y corte r

• El significado físico de este parámetro está dado por la expresión r = K_i/G_i
• K_i se corresponde con el módulo de tangente de compresión de compresión isotrópica de acuerdo con la línea de consolidación normal
• G_i se corresponde con el módulo tangente de corte para la prueba de corte sin drenaje asumiendo el mismo estado de tensión
• Parámetro r puede determinarse por un estudio paramétrico de ensayo triaxial de corte
• Los valores más comunes son en el rango de 0,05 a 0,7

Configuración del estado inicial del suelo

En arcilla hipoplástica el estado actual de suelo está asociado con la compactación corriente representada por la relación de vacío. El modelo de implementación permite, ya sea para la imputación de la relación de vacíos directa o para el cálculo a partir de la relación introducida preconsolidación OCR. En el primer caso, el valor de entrada de e₀ corresponde a la relación de vacío medido en una muestra sin carga extraída de una profundidad dada, véase la Figura 4a. En el segundo caso, el valor de OCR se especifica. Este parámetro representa la relación entre la tensión media en la NCL y la tensión media inicial, véase la Figura 4b.

Cuando se inicializa la tarea con el procedimiento K₀, el estado de tensión inicial al comienzo de la segunda etapa se asigna al estado de tensión actual. Si se adopta el análisis clásico en la primer etapa ((el modelo de arcilla hipoplásico se introduce ya en la primer etapa de cálculo) donde el suelo se carga por su propio peso, el valor de la tensión inicial es P_in= 1 kPa se asume y se mantiene e_{curr =} e₀ . Proporcionando un material diferente (por ejemplo considerado en la primera etapa de cálculo) se sustituye por el modelo de arcilla hipoplástica, se adoptó el estado inicial de tensión derivado en la etapa anterior. Recordemos que cuando se utiliza material elástico en la primera etapa de cálculo el estado de tensión resultante corresponde a los resultados proporcionados por el procedimiento de K_o para K_o (ν es la relación de Poisson).

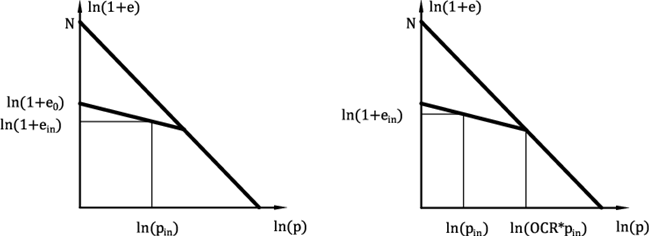Figura 4: relación al vacío inicial – (a) entrada directa de la relación al vacío. (b) inicialización po OCR

Se desprende de la figura 5 que para suelos normalmente consolidados el estado para el cual OCR = 1,0 corresponde a una consolidación isotrópica sólo, para K_o = 1,0. Si el suelo experimenta un estado de tensión desviadora distinto de cero el OCR correspondiente para un suelo normalmente consolidado es mayor que 1,0. Un valor exacto depende de parámetros del suelo y de la trayectoria de la tensión (el valor de K_o). La Figura 5 muestra la dependencia de la mínima para diversos valores de K_o y diferentes tipos de suelos arcillosos. Los valores particulares también se almacenan en la Tabla 1. Los parámetros de los materiales básicos de este conjunto de suelos se enumeran en la Tabla 2.

La elección de OCR = 1,0 para suelos normalmente consolidados con K_o distinto de 1.0 crea un estado de tensión no aceptable que puede resultar en la pérdida de la convergencia.

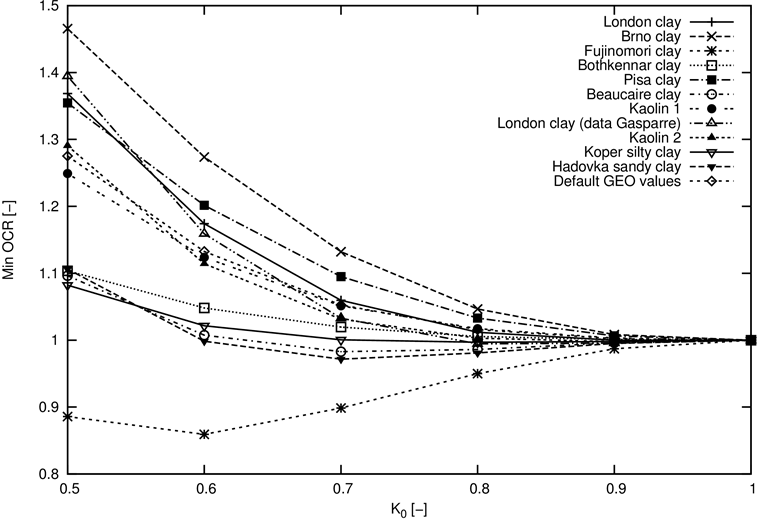Figura 5: Dependencia de OCR en el coeficiente de presión de tierra en reposo Ko

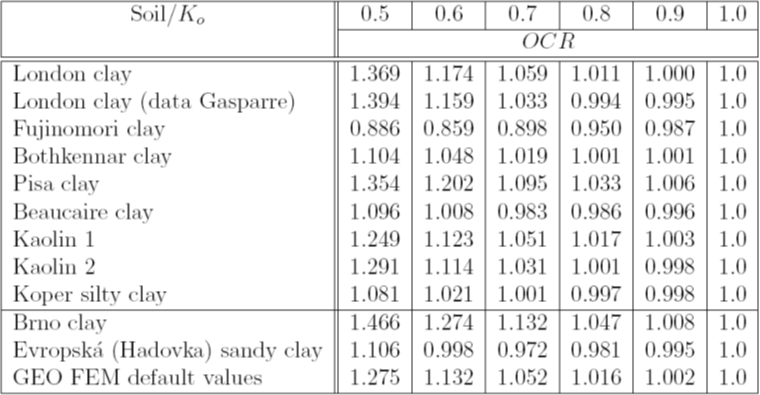Table 1: Índice de consolidación OCR del suelo seleccionado como función del valore Ko

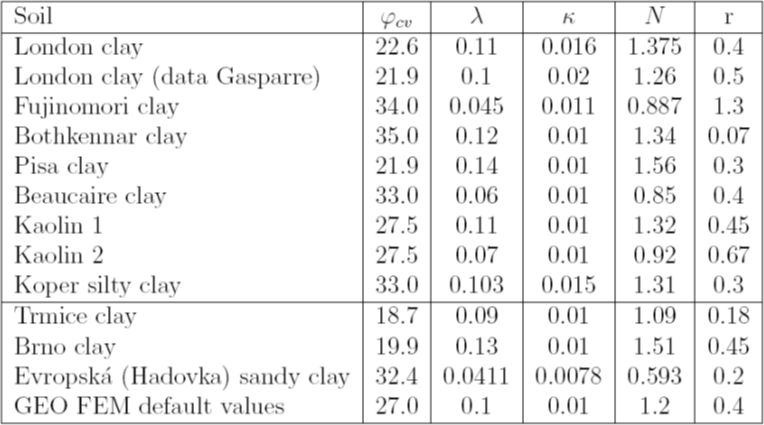Tabla 2: Parámetros de materiales de los suelos seleccionados

Tensión intergranular La versión básica del modelo es adecuado en los análisis con una dirección predominante de la trayectoria de carga de estrés. En los casos con carga cíclica (carga-descarga-recarga) es más adecuado utilizar una fórmula avanzada con el concepto de la tensión intergranular. Esto permite restringir un aumento inaceptable de la deformación que surge durante pequeños cambios permanentes en la carga de repetición (de trinquete). Ingresando de la tensión intergranular permite el modelado de grande rigidez, que las arcillas experimentan durante pequeñas deformaciones. Esta opción no es parte en ninguno de los otros modelos implementados en GEO FEM. El concepto de tensión intergranular asume que la deformación total del suelo se compone de una pequeña deformación de una capa intergranular (tensión intergranular) y la deformación causada por el deslizamiento mutuo de los granos. Cambiando la ruta de carga primero se cambia la tensión intergranular. Al alcanzar el valor límite de la tensión intergranular, la deformación asociada con el movimiento de los granos se fija. Adoptar el concepto de tensión intergranular requiere cinco parámetros adicionales:

• Rango de tensión elástica intergranular R
• Parámetros m_R y m_T control de la rigidez de pequeñas deformaciones
• Parámetros beta βr y χ controlan el grado de degradación de rigidez con tensión cortante creciente

Estos parámetros son calibrados después de conocer los datos del material del modelo básico hipoplástico.

Margen de deformación elástica intergranular R

• Se determina el rango de tensión intergranular máximo
• Se puede determinarse por un estudio paramétrico de la curva de degradación G = G (ε_s), Figura 5
• Alternativamente, puede ser considerado como material independiente constante R = 10^-4
• Los valores más comunes están en el rango de 2*10^-5 - 1*10^-4

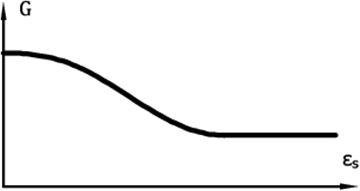Figura 5: Curva describiendo la pérdida de rigidez del módulo de corte

Parámetro m_R

• Se determina la magnitud del módulo de corte cuando se cambia la ruta de carga en el plano meridial (σ_m - J) o 180°
• La relación lineal entre el parámetro m_R y el módulo de corte inicial G₀ es proporcionada por G₀ = p*(m_r/(r * λ^*)
• El módulo de corte inicial se puede determinar a partir de la medición de la propagación de la onda de cizalla [2]
• Los valores más comunes son en el rango de 4,0 a 20,0

Parámetro m_T

• Se determina la magnitud del módulo de corte cuando se cambia la ruta de carga en el plano meridial (σ_m - J) o 90°
• Se mantiene m_R/m_T = G₀/G₉₀
• El radio de los módulos iniciales pueden estimarse a partir de la relación de estos módulos para el valor más grande de tensión. El valor del radio m_R/m_T está comúnmente en el rango de 1.0 – 2.0
• Los valores más comunes de m_T están en el rango de 2.0 – 20.0

Parámeteros β_r y χ

• Determinar la tasa de degradación de la rigidez con tensión cortante en crecimiento
• Se puede determinarse por un estudio paramétrico de la curva de degradación G = G(ε_s)
• Los valores más comunes del parámetro β_r están en el rango de 0.05 – 0.5
• Los valores más comunes de parámetro χ están en el rango 0.5 – 6

Bibliografía:

[1] D. Mašín, A hypoplastic constitutive model for clays, International Journal for Numerical and Analytical Methods in Geomechanics., 29:311-336, 2005.