Modèles de matériau dans l'analyse des écoulements
L’analyse des écoulements en régime permanent est régie par la loi de Darcy qui spécifie la relation entre la vitesse d’écoulement et le gradient de la charge hydraulique. La version actuelle du programme suppose des valeurs constantes des coefficients de perméabilité indépendants de la pression interstitielle.
Le programme impose également de valoriser l'indice des vides initial e0 permettant de déterminer la porosité courante n, puis la vitesse réelle de l’eau traversant uniquement les pores vs = v/n, où v est la vitesse moyenne d’écoulement dans toute la zone d’infiltration. En règle générale, à l'indice des vides vérifiant e0 = 1 correspond une porosité du sol valant n = 50%.
En introduisant le coefficient de perméabilité relative de Kr, le programme permet de suivre la zone de transition entre la région complètement saturée (S = 1, Kr = 1) et la région non saturée (Kr → 0) du corps de sol. A titre d'exemple, nous pouvons considérer le problème du flux non confiné. Le processus de suivi de la zone de transition est régi par l’un des trois modèles de zone de transition déterminant l’évolution du coefficient de perméabilité relative de Kr en fonction de la hauteur de pression interstitielle, voir Figures.
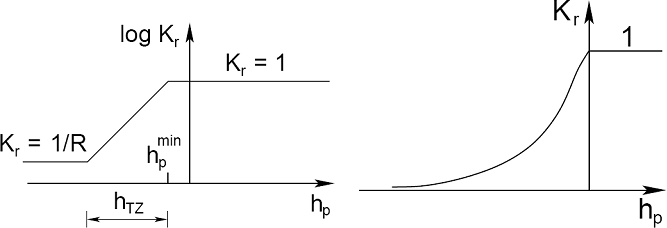 (a) modèle Log-linéaire [1], (b) modèle de Van Genuchten [2]
(a) modèle Log-linéaire [1], (b) modèle de Van Genuchten [2]
Modèle Log-linéaire
Le modèle log-linéaire de zone de transition, décrit par exemple dans [1], est défini par les paramètres suivants :
hpmin | - | valeur minimale de la hauteur de pression dans une région complètement saturée [kPa] | |
hTZ | - | largeur de la zone de transition [m] | |
R | - | paramètre de réduction, un nombre suffisamment grand R = 100 à 1000 [-], valeur par défaut R = 1000 [-] |
Le coefficient de perméabilité relative Kr est donné par :
![]()
Modèle de Gardner
Ceci est un modèle équivalent dépendant uniquement d'un seul paramètre α [1/m]. Le coefficient de perméabilité relative Kr est dans ce cas donné par [4] :
![]()
Modèle de Van Genuchten
Dans ce cas, la valeur du coefficient de perméabilité relative Kr est donnée par :
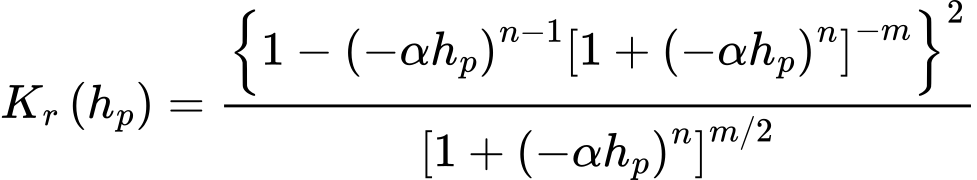
où α [1/m], n > 1 et m = 1 - 1/n sont les paramètres du modèle. Leurs valeurs peuvent être obtenues à partir des courbes de rétention approchées résultant de mesures en laboratoire par :
![]()
![]()
où : | Ssat | - | degré de saturation d'un sol complètement saturé, valeur par défaut Ssat = 1 |
Sr | - | degré de saturation résiduel | |
Θ | - | teneur en eau normalisée |
Le paramètre Θ est en général fourni par :
![]()
où : | θr | - | teneur en eau résiduelle [m3/m3] |
θS | - | teneur en eau d'un sol complètement saturé [m3/m3] |
Le degré actuel de saturation S peut être exprimé comme le rapport de la teneur en eau θ et de la porosité n comme suit (il est nécessaire de distinguer entre n représentant la porosité et n qui apparaît dans le modèle de van Genuchten, ce sont deux variables différentes) :
![]()
Les modèles Log-linéaire et de Gardner adoptent une version simplifiée du modèle van Genuchten selon [5] :
![]()
où b > 0 [-] est un paramètre d'ajustement permettant une meilleure approximation des données de rétention d'un sol donné.
Nous recommandons les tableaux de paramètres suivants qui sont réellement utilisés dans le programme. Ces paramètres sont dérivés de ceux donnés dans les tableaux d'origine.
Les valeurs optimales des paramètres du modèle de van Genuchten pour diverses classifications basées sur l'USDA et la FAO sont présentées dans les tableaux suivants.
Tableau des coefficients de régression de Van Genuchten pour les classes de taille de grains de l'USDA (1991)
Sol (taille des grains) | Ksat [m/day] | RETC | Rosetta | ||||||
e [-] | Sr [-] | α [1/m] | n [-] | e [-] | Sr [-] | α [1/m] | n [-] | ||
Sable | 7,13 | 0,75 | 0,11 | 14,5 | 2,68 | 0,60 | 0,14 | 3,5 | 3,18 |
Sable loameux | 3,50 | 0,70 | 0,14 | 12,4 | 2,28 | 0,64 | 0,13 | 3,5 | 1,747 |
Loam sableux | 1,06 | 0,70 | 0,16 | 7,5 | 1,89 | 0,63 | 0,10 | 2,7 | 1,448 |
Loam | 0,25 | 0,75 | 0,18 | 3,6 | 1,56 | 0,66 | 0,15 | 1,1 | 1,474 |
Silt | 0,06 | 0,85 | 0,07 | 1,6 | 1,37 | 0,96 | 0,10 | 0,7 | 1,677 |
Loam limoneux | 0,11 | 0,82 | 0,15 | 2,0 | 1,41 | 0,78 | 0,15 | 0,5 | 1,663 |
Loam sablo-argileux | 0,314 | 0,64 | 0,26 | 5,9 | 1,48 | 0,62 | 0,16 | 2,1 | 1,33 |
Loam argileux | 0,062 | 0,70 | 0,23 | 1,9 | 1,31 | 0,79 | 0,18 | 1,6 | 1,415 |
Loam limono-argileux | 0,017 | 0,75 | 0,21 | 1,0 | 1,23 | 0,93 | 0,19 | 0,8 | 1,52 |
Argile sableuse | 0,029 | 0,61 | 0,26 | 2,7 | 1,23 | 0,63 | 0,30 | 3,3 | 1,207 |
Argile limoneuse | 0,0048 | 0,56 | 0,19 | 0,5 | 1,09 | 0,93 | 0,23 | 1,6 | 1,321 |
Argile | 0,048 | 0,61 | 0,18 | 0,8 | 1,09 | 0,85 | 0,21 | 1,5 | 1,253 |
Tableau des coefficients de régression de Van Genuchten pour les classes de taille de grains de la FAO (1998)
Sol (taille des grains) | Ksat [m/day] | e [-] | Sr [-] | α [1/m] | n [-] |
Sol superficiel (jusqu'à 1 m de profondeur) | |||||
Grossier (C) | 0,600 | 0,68 | 0,062 | 3,83 | 1,3774 |
Moyen (M) | 0,121 | 0,78 | 0,023 | 3,14 | 1,1804 |
Moyennement fin (MF) | 0,023 | 0,75 | 0,023 | 0,83 | 1,2539 |
Fin (F) | 0,248 | 1,08 | 0,019 | 3,67 | 1,0120 |
Très fin (VF) | 0,150 | 0,78 | 0,016 | 2,65 | 1,1033 |
Sol en profondeur (> 1 m) | |||||
Grossier (C) | 0,700 | 0,58 | 0,068 | 4,30 | 1,5206 |
Moyen (M) | 0,108 | 065, | 0,026 | 2,49 | 1,1689 |
Moyennement fin (MF) | 0,040 | 0,70 | 0,024 | 0,82 | 1,2179 |
Fin (F) | 0,085 | 0,93 | 0,021 | 1,98 | 1,0861 |
Très fin (VF) | 0,082 | 1,17 | 0,019 | 1,68 | 1,0730 |
Tableau : Système de classification des textures de la FAO
Sol | Définition |
Grossier (C) Moyen (M) | argile < 18% et sable > 65% 18%< argile < 35% et 15%< sable ou: argile < 18% et 15%< sable < 65% |
Moyennement fin (MF) | argile < 35% et sable < 15% |
Fin (F) | 35%< argile < 60% |
Très fin (VF) | 60%< argile |
Littérature :
Details can be found in [2].
[1] D.M. Potts, L. Zdravkovič, Finite element analysis in geotechnical engineering - theory, Thomas Telford, London, 1999.
[2] M. Th. Van Genuchten, A closed formulation for predicting the hydraulic conductivity of unsaturated soils, Journal Soil Science Society of America 44, 239-259, 1988..
[3] M. Šejnoha, Finite element analysis in geotechnical design, to appear (2015)
[4] W. R. Gardner, Some steady-state solutions of the unsaturated moisture flow equation to evaporation from a water table, Soil Science 85(4), 228-232, 1958.
[5] M. Šejnoha, T. Janda, H. Pruška, M. Brouček, Metoda konečných prvků v geomechanice: Teoretické základy a inženýrské aplikace, předpokládaný rok vydání (2015)
[6] USDA 1951. Soil Survey Manual. Soil Conservation Service. U.S. Department of Agriculture Handbook No. 18. US Government Printing Office. Washington DC.
[7] Wösten, J.H.M., et. al. 1998. Using existing soil data to derive hydraulic parameters for simulation models in environmental studies and in land use planning. Final Report on the European Union Funded project. DLO Winand Staring Centre. Report 156, Wageningen, NL. p. 106. ISSN 0927-04537.