Drucker-Prager
O modelo material de Drucker-Prager é o modelo mais simples que pode ser adotado para a modelação da resposta não linear de solos. Contrariamente ao modelo de Mohr-Coulomb, a superfície de cedência de Drucker-Prager yield é suave e define um cone cilíndrico no espaço principal de tensão. De acordo com a figura seguintes, a superfície de cedência depende da tensão efetiva média σmeff, de forma semelhante ao modelo de Mohr-Coulomb. A versão atual do odelo implementado no GEO5 MEF baseia-se na extensão triaxial. Por outras palavras, a projeção da superfície de cedência fDP em um plano de desvio atravessa vértices internos do hexágono de Mohr-Coulomb, θ = - 30°, onde θ é o ângulo de Lode.
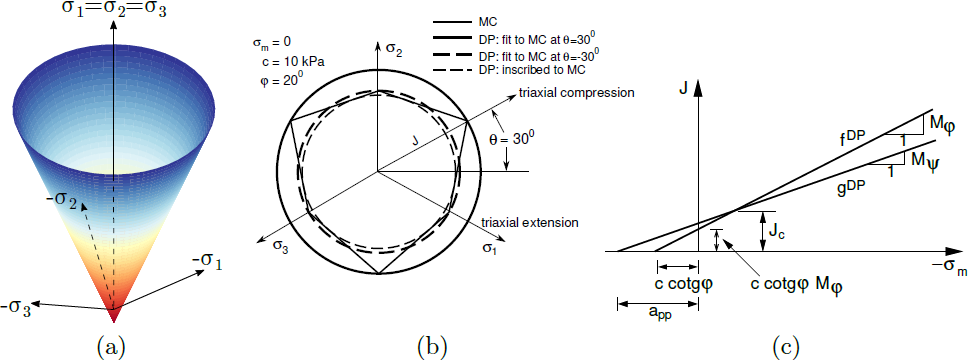 a) superfície de cedência no espaço de tensão principal, b) projeção no plano de desvio e c) no plano meridiano
a) superfície de cedência no espaço de tensão principal, b) projeção no plano de desvio e c) no plano meridiano
O modelo de Drucker-Prager permite considerar a dilatação dos materiais (desenvolvimento de deformações plásticas volumétricas positivas durante o cisalhamento) ao introduzir o ângulo de dilatação ψ. O desenvolvimento de deformações plásticas é, geralmente, controlado pelo potencial plástico gDP. Enquanto a inclinação da superfície de cedência no plano meridiano é dada pelo ângulo de atrito interno Mφ = Mφ(φ), a inclinação da superfície de potencial plástico depende do ângulo de dilatação Mψ = Mψ(ψ). A condição ψ = φ corresponde à condição verificada. Pode encontrar mais detalhes no manual teórico. Dado que o solo atinge, eventualmente, o estado crítico (deixa de haver incremente na deformação plástica volumétrica durante o cisalhamento plástico), é aconselhável limitar a extensão da dilatação. Isto implica a introdução do índice de vazios máximo emax, para o qual se assume ψ = 0 quando se atinge o estado crítico. Pode encontrar um exemplo ilustrativo aqui. A forma como a definição do valor do ângulo de dilatação influencia a estimativa da resposta do solo em comparação com o seu comportamento real é apresentado aqui. Para melhor clareza, a imagem seguinte apresenta uma representação gráfica da evolução da deformação volumétrica com a dilatação limitada.
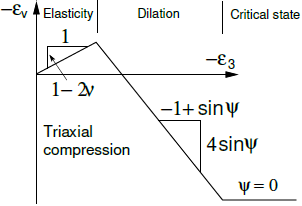 Desenvolvimento de deformação plástica volumétrica com limitação da dilatação
Desenvolvimento de deformação plástica volumétrica com limitação da dilatação
Os parâmetros materiais base que definem o modelo de Drucker-Prager são apresentados na tabela seguinte. Estes parâmetros podem ser adotados ao realizar análises para condições drenadas ou em casos de condições não drenadas, Tipo (1): análise para tensões efetivas (cef, φef). Ao escolher o Tipo (2): análise para tensões efetivas (Su), o valor da coesão efetiva c é substituído pelo valor da resistência ao cisalhamento não drenada Su. O valor do ângulo de atrito interno efetivo φ = φu passa a zero, φ = 0. A superfície de cedência de The Drucker-Prager é, então, substituída pela superfície de cedência de Mises - ver em baixo. No entanto, os parâmetros de rigidez são assumidos como efetivos. Em condições não drenadas é, geralmente, expectável que o solo não experiencie dilatação. O ângulo de dilatação ψ = 0 é adotado em ambos os casos.
A partir da tabela dos parâmetros materiais é evidente que o modelo de Drucker-Prager, tal como o modelo elástico modificado, considera uma resposta do solo diferente para o carregamento inicial e para o relaxamento/recarregamento, devido à introdução do módulo de relaxamento/recarregamento Eur - ver também o modelo de Mohr-Coulomb.
Símbolo | Unidade | Descrição | |
| [MPa] | Módulo de elasticidade | |
| [MPa] | Módulo de relaxamento/recarregamento | |
| [-] | Coeficiente de Poisson | |
| [kPa] | Coeficiente de coesão efetivo | |
| [°] | Ângulo de atrito interno efetivo | |
| [°] | Ângulo de dilatação | |
| [kN/m3] | Peso volúmico | |
| [-] | Índice de vazios inicial, correspondente ao estado do final da 1a etapa de cálculo | |
| [-] | Índice de vazios máximo, para terminar a dilatação (ao limitar a dilatação) | |
| [1/K] | Coeficiente de dilatação térmica (quando são considerados efeitos de temperatura) |
Ao escolher condições não drenadas do Tipo (3): análise para tensões totais Su, a superfície de cedência de Drucker-Prager torna a ser substituída pela superfície de cedência de Mises. De forma idêntica, a superfície de cedência de Mohr-Coulomb é substituída pela superfície de cedência de Tresca. A figura seguinte apresenta uma representação gráfica. Esta opção considera que φ = ψ = 0, o que corresponde à condição verificada. Ao modelar materiais incompressíveis volumetricamente, assume-se que o valor do Coeficiente de Poisson varia entre 0.49 - 0.499. De notar que definir o valor do Coeficiente de Poisson próximo de 0.5 pode resultar em instabilidade numéricas, ou, na melhor das hipóteses, os resultados serão pouco precisos. Pode encontrar mais detalhes no manual teórico.
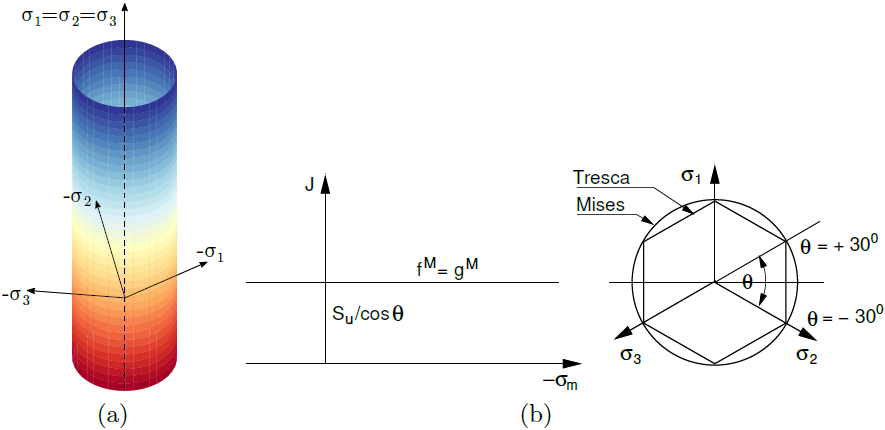 a) superfície de cedência no espaço de tensão principal, b) projeção no plano de desvio e c) no plano meridiano
a) superfície de cedência no espaço de tensão principal, b) projeção no plano de desvio e c) no plano meridiano
A tabela seguinte apresenta os parâmetros materiais que definem a superfície de cedência de Mises de Tresca. No caso da superfície de cedência de Mises, o valor do ângulo de Lode θ é constante e igual a θ = ± 30°.
Símbolo | Unidade | Descrição | |
Eu | [Pa] | Módulo de elasticidade não drenado | |
Su | [Pa] | Resistência ao cisalhamento não drenada | |
ν | [-] | Coeficiente de Poisson assumido dentro do intervalo 0.49 - 0.499 | |
γ | [kN/m3] | Peso volúmico | |
α | [1/K] | Coeficiente de dilatação térmica (quando são considerados efeitos de temperatura) |
O modelo de Drucker-Prager permite, tal como o modelo de Mohr-Coulomb, realizar a análise de estabilidade. Podem ser realizadas análises de estabilidade de taludes padrão como análises de estabilidade para etapas de construção específicas. Em ambos os casos, a tarefa é resolvida através da redução gradual dos parâmetros de resistência ao cisalhamento c, φ, com a introdução de um parâmetro de redução ζ, e forma a que
![]()
onde c, φ representam os parâmetros da resistência ao cisalhamento atual e cd, φd representam os parâmetros reduzidos. O Fator de Segurança FS é dado por
![]()
De forma idêntica, o ângulo de dilatação também é reduzido ψ de forma a que ψ ≠ 0.
A implementação do modelo material de Drucker-Prager no programa GEO5 MEF está descrito em detalhe no manual teórico.