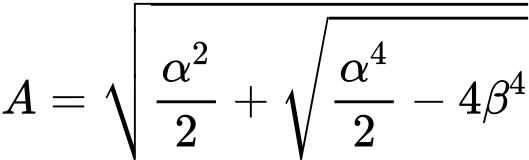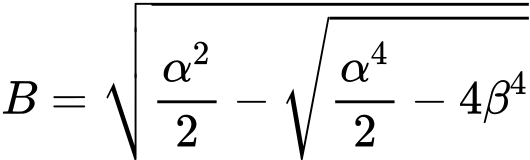Método Geométrico (Euler)
O solo que envolve a microestaca é representado, no programa, pelo módulo de reação do subsoloEp (constante de Winkler k), definido na janela "Cálculo da secção". A figura mostra um modelo da estrutura.
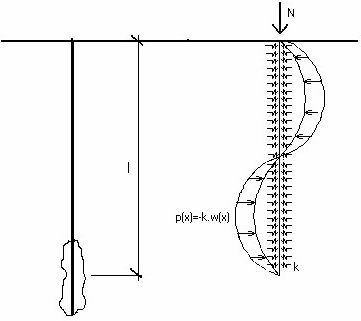 Modelo da estrutura
Modelo da estrutura
Para uma microestaca à compressão, é expectável que ocorra um número variável de meias ondas, dependendo da geometria e rigidez da estrutura e do solo envolvente. A solução para este caso é obtida através da equação da flexão de uma viga plana.
![]()
Após alguma manipulação, a equação para a flexão pode ser expressa como:
| |
onde: | |
| |
| |
| |
|
As constantes de integração C1-C4 são obtidas a partir das quatro condições de fronteira, consoante os apoios assumidos.
A força crítica Ncr é calculada através da fórmula (in [1]):
![]()
onde: | Ei | - | módulo de Elasticidade da secção transversal ideal |
Ii | - | momento de inércia da secção transversal ideal | |
lp | - | comprimento efetivo da microestaca (comprimento livre + 1/2 comprimento da raiz) | |
Er | - | ||
n | - | número de meias ondas |
A força crítica Ncr é considerada como a função mínima (2). Esta é alcançada para o comprimento de meia onda:
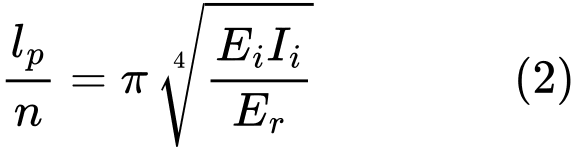
O número de meias ondas n baseia-se na fórmula (3):
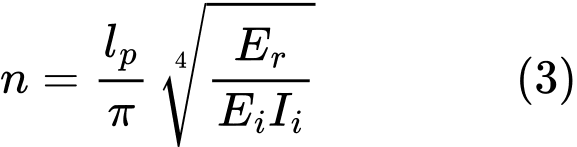
Caso uma parte da microestaca esteja acima da superfície do terreno (deslocamento da cabeça da estaca), os valores reduzidos de n e Er são calculados de acordo com:
![]()
![]()
onde: | lv | - | comprimento da microestaca acima da superfície do terreno |
Assumindo a condição rótula-rótula, deve-se utilizar a equação seguinte:
![]()
Assumindo a condição rótula-apoio fixo, deve-se utilizar a equação seguinte:
![]()
Bibliografia:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936