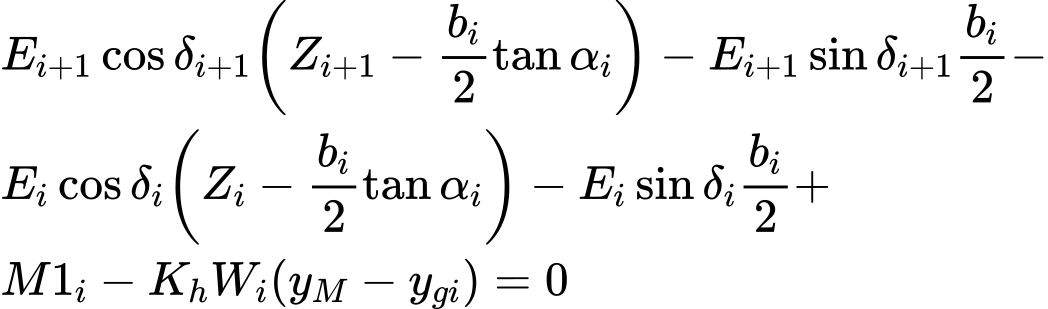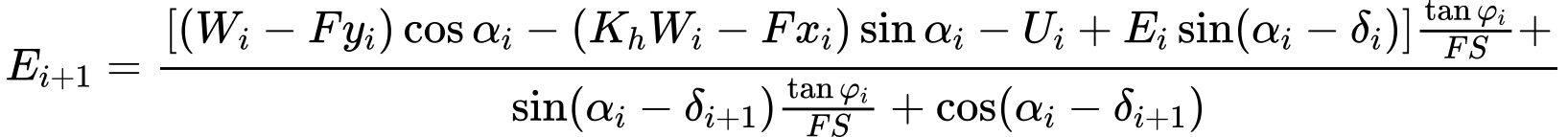Джанбу
Метод Джанбу - это метод предельного равновесия, работающий методом отсеков. Метод основан на удовлетворении равновесия сил и моментов на отдельных блоках (не выполнено только условие момента на последнем самом верхнем блоке). Блоки возникают путем разделения области грунта над поверхностью скольжения плоскостями раздела.
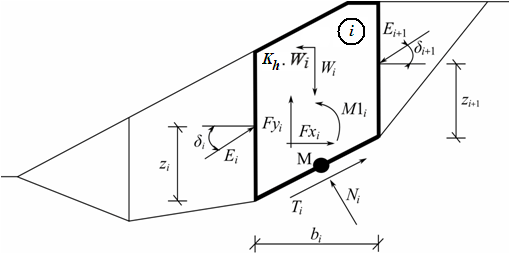Статистическая схема: метод Джанбу
Предполагается, что каждый блок испытывает следующие усиления:
Wi | - | вес блока, включая напряжение материала, имеющего свойство блока, в т.ч. воздействие коэффициента вертикального землетрясения Kv |
Kh*Wi | - | горизонтальная инерционная сила, представляющая действие землетрясения, Kh - коэффициент горизонтального ускорения во время землетрясения |
Ni | - | нормальная сила на поверхности скольжения |
Ti | - | сила сдвига на поверхности скольжения |
Ei ,Ei+1 | - | силы, приложенные соседними блоками, они наклонены от горизонтальной поверхности на угол δi и δi+1 соответственно, и находящиеся на высоте zi и. zi+1 соответственно над поверхностью скольжения |
Fxi Fyi | - | другие горизонтальные и вертикальные силы, действующие на блок |
M1i | - | момент от сил Fxi , Fyi, вращающихся вокруг точки M, которая является центром i-ого сегмента поверхности скольжения |
Ui | - | равнодействующая порового давления на i-ом сегменте поверхности скольжения |
Для расчета предельного равновесия сил и моментов на отдельных блоках по методу Джанбу используются следующие допущения:
- | плоскости раздела между блоками всегда вертикальны |
- | линия действия веса блока Wi проходит через центр i-ого сегмента поверхности скольжения, представленного точкой M |
- | нормальная сила Ni действует в центре i-ого сегмента поверхности скольжения, в точке М |
- | принимается положение zi сил Ei, действующих между блоками, на конечных точках поверхности скольжения z=0 |
Выбор положения zi может иметь значительное влияние на конвергенцию метода. При неверном предположении положения zi для данного уклона, может оказаться невозможным удовлетворить условия равновесия (алгоритм не сходится).Высота zi над поверхностью скольжения устанавливается примерно на 1/3 от высоты стыка между блоками. В случае неудовлетворения условий равновесия, алгоритм переносит высоты на иную позицию, т.е. немного выше в пределах пассивной зоны, около основания, и выше в пределах активной зоны, около гребня уклона.
Решение принимает следующие выражения:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
где: | φi | - | угол внутреннего трения грунта на сегменте поверхности скольжения |
ci | - | удельное сцепление грунта на сегменте поверхности скольжения | |
αi | - | уклон сегмента поверхности скольжения |
Уравнение (1) представляет отношение между эффективным и общим значением нормальной силы, действующей на поверхность скольжения. Уравнение (2) соответствует условию Мора-Кулона, представляющего отношение между нормальной и сдвиговой силами на данном сегменте поверхности скольжения. Уравнение (3) представляет уравнение равновесия силы в направлении под прямым углом к i-ому сегменту поверхности скольжению, а уравнение (4) представляет силу равновесия вдоль i-ого сегмента поверхности скольжения. SF - коэффициент надежности, который используется для приведения параметров грунта. Уравнение (5) соответствует уравнению момента равновесия вокруг точки M, где ygi - вертикальная координата точки приложения веса блока, а yM - вертикальная координата точки M.
Изменяя уравнения (3) и (4), получаем следующую рекурсивную формулу (6):
| (6) |
Эта формула позволяет рассчитать все силы Ei, действующие между блоками для данных значений δ и FS. Это решение допускает, что в начале поверхности скольжения значение E известно и равно E1=0.
Формула для расчета угла δi (7) выводится из уравнения момента равновесия (5):
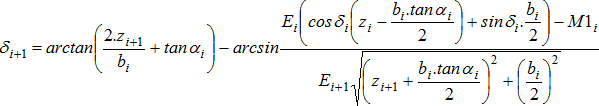(7)
Эта формула позволяет рассчитать углы δi для всех значений zi, зная значения в конечных точках поверхности скольжения δ = 0.
Коэффициент надежности SF определяется при помощи следующего итерационного процесса:
1. | Начальное значение углов устанавливается на 0, δi = 0, а положения zi - на примерно 1/3 высоты стыка. |
2. | Коэффициент надежности SF для данного значения δi следует из уравнения (6), при этом допускается значение En+1 = 0 в конце поверхности скольжения. |
3. | Значение δi рассчитывается уравнением (7) с помощью значений Ei, определенных на предыдущем этапе. |
4. | Этапы 2 и 3 повторяются до тех пор, пока значение FS не измениться. |
Для обеспечения успешного процесса итерации необходимо избегать неустойчивых условий. Такие нестабильности появляются в точках, где имеет место деление на 0 в выражении (6), например:
Еще одним способом предупредить цифровою нестабильность является проверка параметра mα: должно выполняться следующее условие:
Таким образом, перед началом итерации необходимо найти наивысшие показатели критических значений (SFmin), удовлетворяющих выше указанные условия. Значения ниже данного критического значения SFmin находятся в области неустойчивого решения, таким образом, итерация начинается с установки SF на значение «слегка» выше SFmin, и все получаемые значения SF из итерации выше, чем SFmin.
В общем можно сказать, что сложные методы труднее подвергаются конвергенции чем более простые методы (Bishop, Fellenius). Проблемы с конвергенцией возникают напр., на участках поверхности скольжения повышенной крутизны, сложной геометрии, при резком увеличении пригрузки и т.п. В случае, что расчёт не даёт результата, рекомендуется немного изменить задание, напр., уменьшить крутизну, в поверхность скольжения добавить больше точек и т.п. или выполнить расчёт по более простому методу.
Литература:
Janbu, N. 1954. Application of Composite Slip Surface for Stability Analysis. European Conference on Stability Analysis, Stockholm, Sweden.
Janbu, N. 1973. Slope Stability Computations. Embankment Dam Engineering - Casagrande Volume, R.C. Hirschfeld and S.J. Poulos, eds., John Wiley and Sons, New York, pp 47-86.