Метод ITF
Метод IT - это метод предельного равновесия.( Метод неуравновешенных сдвигающих сил). Он основан на условии суммирования сил на отдельных блоках и не учитывает условие момента. Принцип метода и принятые допущения очевидны на рис. 1.
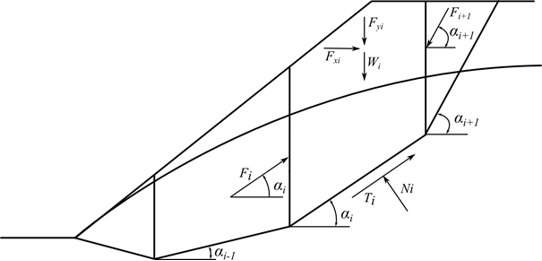 Рис. 1 Схема сил, действующих на блоке
Рис. 1 Схема сил, действующих на блоке
Воздействие сил на блок основано на следующих предположениях:
где: | Wi | - | вес блока, для части блока, находящейся под водой, вес рассчитывается, исходя из объемного веса водонасыщенного грунта γsat |
Fyi | - | другие вертикальные нагрузки, действующие на блок | |
Fxi | - | другие горизонтальные нагрузки, действующие на блок | |
Fi, Fi+1 | - | силы между блоками, действующие под углами αi и αi+1 |
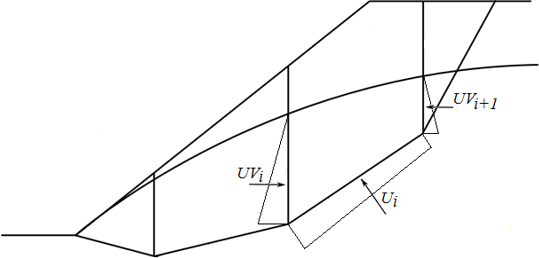 Рис. 2 Схема воздействия порового давления на блок
Рис. 2 Схема воздействия порового давления на блок
Ui | - | равнодействующая порового давления на сегменте поверхности скольжения | |
UVi,UVi+1 | - | равнодействующая порового давления на боковых рёбрах блока |
В расчёте силы UVi и UVi+1 включены в горизонтальные силы Fxi.
Уравнение равновесия сил в нормальном направлении к сегменту поверхности скольжения дает отношение:
![]()
Между силами на сегменте поверхности скольжения справедливо отношение:
![]()
где: | φi | - | угол внутреннего трения грунта |
ci | - | сцепление грунта | |
| li | - | длина сегмента поверхности скольжения на i-блоке |
Из уравнения равновесия сил в направлении i-сегмента поверхности скольжения (под углом α) вытекает отношение для величины силы между блоками Fi, в виде:
![]()
Подстановкой уравнений (1) и (2) в отношение (3):
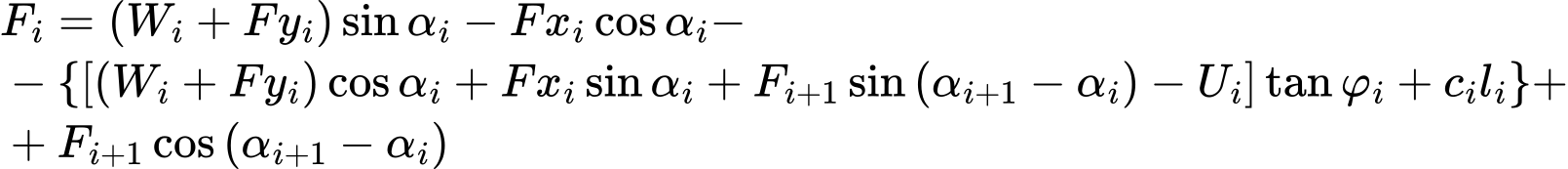
и формальными операциями получаем окончательную форму уравнения (условия] равновесия, как:
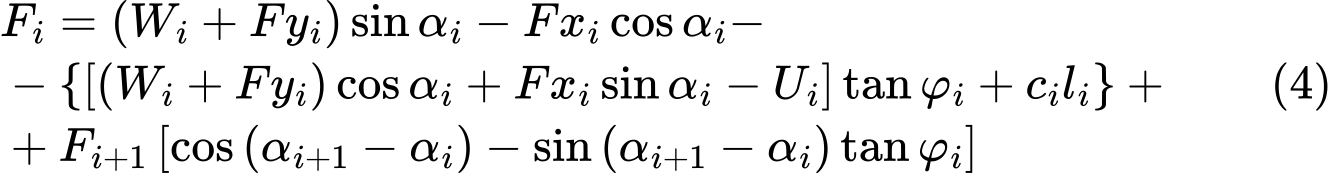
Условие равновесия будет соблюдено путем введения в анализ коэффициента устойчивости SF. Коэффициент устойчивости вводится в расчет путем деления им прочностных характеристик грунта c и tanφ Уравнение (4) принимает вид:
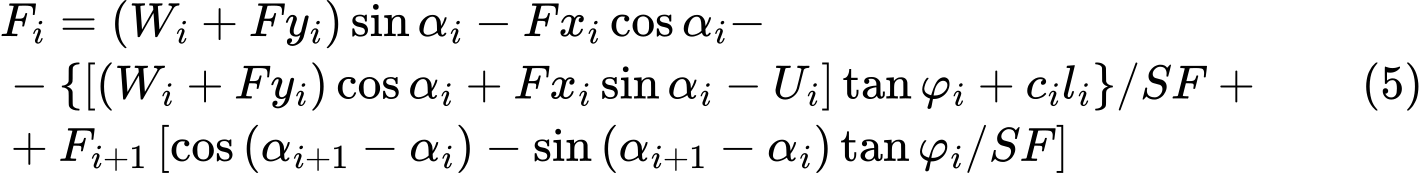
По уравнению (5) затем рассчитываем коэффициент (степень) устойчивости SF путём итерации. Итерация проходит так, что к самой высокой (конечной) точке поверхности скольжения прикладываем силу Fn равную 0 kN. Для выбранной степени стабильности SF рассчитываем по уравнению (5) величины всех сил между блоками Fi. Операция повторяется для разных значений степени (коэффициента) устойчивости SF до тех пор, пока не находим SF, сила F0 которого в начале поверхности скольжения (у подошвы откоса) равна 0 kN.
Расчёты для поверхности скольжения не учитывают (исключают) растягивающие нагрузки. Но если при расчете равновесия получаем отрицательные значения нормальной силы Ni, что свидетельствует о том, что здесь грунт испытывает растягивающее напряжение, то в дальнейших расчётах принимается нулевое значение этой силы, а сдвигающее усилие Ti на сегменте поверхности скольжения определяется только по сцеплению грунта.
Метод ITF относительно чувствителен к форме поверхности скольжения. В случае, что поверхность скольжения резко меняет свое направление, (“перелом или поворот формы“), то коэффициент, как правило, получатся завышенный. Рекомендуется, чтобы разница угла наклона между отдельными сегментами поверхности скольжения составляла не более 10°. Это автоматически проверяется программой, и если разница углов наклона оказывается больше, программа выдает сообщение о том, что результаты могут не соответствовать реальности. Обычно эта проблема не касается кругло-цилиндрической поверхности скольжения, но ее следует иметь в виду в случае многоугольных (полигональных) поверхностей скольжения.
Метод ITF - явное решение задачи
Явное решение метода ITF - предполагает другой способ ввода степени (коэффициента) устойчивости в анализ. Математическое решение, тем самым, не требует итераций, а результирующий коэффициент устойчивости вычисляется непосредственно за один шаг. При явном решении задачи коэффициент устойчивости, как правило, получается завышенным, что может полностью обесценить решение задач, особенно когда расчёт касается многоугольных (полигональных) поверхностей скольжения с резкими изменениями направления.
Решение основано на уравнении равновесия (4), в которое вводим коэффициент устойчивости SF, умножая на него активные составляющие сил, т.е. те составляющие, которые работают в направлении оползания. Условие равновесия приобретает вид :
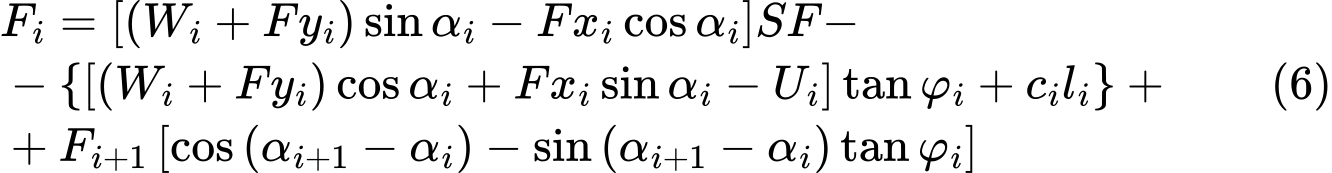
Для наглядности вводим составляющую активных сил, как:
![]()
далее, составляющую пассивных сил, как:
![]()
и вспомогательную функцию:
![]()
Уравнение (6) можно выразить в более краткой форме, как:
![]()
Отталкиваемся от известного нам значения силы Fn = 0 и строим выражения для межблоковых сил F:
![]()
![]()
![]()
и т.д.
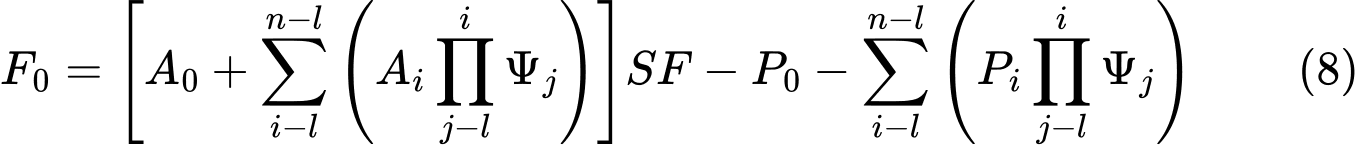
Ввиду того, что сила F0 на нижнем конце поверхности скольжения должна быть равна 0 kN, коэффициент устойчивости SF можно выразить отношением: