Passive Earth Pressure - The Sokolovski Theory
Passive earth pressure follows from the following formula:
![]()
where: | Kpg | - | passive earth pressure coefficient for cohesionless soils |
Kpc | - | passive earth pressure coefficient due to cohesion | |
Kpp | - | passive earth pressure coefficient due to surcharge | |
σz | - | vertical normal total stress |
Individual expressions for determining the magnitude of passive earth pressure and slip surface are introduced in the sequel; the meaning of individual variables is evident from Fig.:
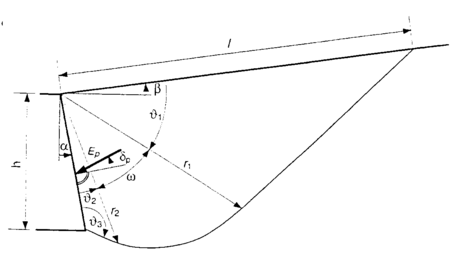 Passive eart pressure slip surface after Sokolovski
Passive eart pressure slip surface after Sokolovski
Angles describing the slip surface:
![]()
![]()
![]()
![]()
![]()
![]()
where: | φ | - | angle of internal friction of soil |
δp | - | ||
β | - | slope inclination |
Slip surface radius vector:
![]()
![]()
![]()
Provided that ω < 0 the both straight edges of the zone r1 and r2 numerically overlap and resulting in the plane slip surface developed in the overlapping region. The coefficients of passive earth pressure Kpg, Kpp, Kpc then follow from:
![]()
![]()
![]()
where: | φ | - | angle of internal friction of soil |
δp | - | ||
α | - | back face inclination of the structure |
![]()
Auxiliary variables: ipg, ipp, ipc, gpg, gpp, gpc, tpg, tpp, tpc
for: | | |
| | |
| | |
| | |
| |
![]()
where:
![]()
For soils with zero value for the angle of internal friction the following expressions are employed to determine the coefficients of passive earth pressure:
![]()
![]()
where:
![]()
![]()
![]()
![]()
Literature:
Sokolovski, V.V., 1960. Statics of Soil Media,Butterworth, London.